Suite Facile

[Sociopath]

Bonjour a tous !

J'ai un petit problème sur les suites...

Voici l'exercice :
On considère la suite U(n) définie par :
U(0) = 1 ; U(n+1) = U(n) + 2n + 3

1°) Etudier la monotonie de la suite U(n) :

2°) a) Démontrer par récurrence que pour tout entier naturel n : U(n) > n²

Ben, voilà merci de bien vouloir m'aider, ne serait-ce que de donner des pistes... :we:

[Fred_Sabonnères]

1) Pour déterminer la monotonie de la suite,calcules la différence 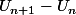et détermines en le signe en fonction de l'indice n.
2) Vérifie la propriété au rang 0.On suppose alors la propriété vraie au rang k.Il faut montrer qu'elle est encore vraie au rang k+1 en calculant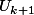 et en introduisant l'inégalité trouvée au rang k à savoir
A+

[Sociopath]

Mouais, on va essayait comme ça...

Merci en tout cas :happy2: