Mesure et intégration : convergende dominée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
par ClaireD » 09 Oct 2007, 19:04
Bonjour,
je m'appelle Claire et je suis étudiante en 3eme année de licence à l'université de Montréal(programme d'échanges).
J'ai un devoir à rendre dans une matière intitulée "mesure et intégration" mais je suis completement bloquée sur une des questions que je vous met ci dessous :
Montrer que:
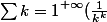 = \int_0^{1} \frac{1}{x^x} dx $)
Si quelqu'un a des idées qu'il n'hésite pas à m'en faire part , elles me seront certainement bien utiles :happy2:
Bonne journée
-
guadalix
- Membre Relatif
- Messages: 405
- Enregistré le: 27 Sep 2007, 08:34
-
par guadalix » 09 Oct 2007, 19:20
Comparaison série intégrale
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 09 Oct 2007, 19:23
Bonjour,
})
Connaissant le développement en série de la fonction exponentielle tu peux en déduire un développement en série de
puis appliquer le théorème de convergence monotone.
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
par ClaireD » 09 Oct 2007, 20:28
ok merci José je vais voir ça :we:
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
par ClaireD » 09 Oct 2007, 23:49
j'ai essayé mais ça ne marche pas....Enfin du moins je finis par me retrouver avec une somme tres bizarre... :mur:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 10 Oct 2007, 13:37
}=\sum\limits_{n=0}^{\infty}\frac{(-x\ln(x))^n}{n!}dx)
donc
)^n}{n!}dx)
et par Beppo-Levi (convergence monotone car :
 \geq 0)
sur [0;1])
^n}{n!}\int_{0}^{1}x^n\ln^n(x)dx)
Ensuite tu essayeras de calculer :
=\int_{0}^{1}x^a\ln^b(x)dx)
en fonction de
)
en faisant une intégration par partie pour trouver
)
et en déduire
dx)
et ce sera fini.
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
par ClaireD » 10 Oct 2007, 23:48
Merci pour ton aide Tize , j'y suis arrivée :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
