Le capitaine Ralph est en
détresse sur le coté ensoleillé de Mercure. La tempéerature de la coque de son vaisseau, lorsquil est
au point (x, y, z), est donnée par la fonction:
T(x, y, z) = exp(;)x2;)2y2;)3z2)
.
Présentement, il est au point (1, 1, 1).
(a) Dans quelle direction devrait-il procéder pour faire baisser sa température le plus rapidement?
(b) Si le vaisseau se déplace a une vitesse de e puissance 8 métres par seconde, a quelle vitesse la température
baissera-t-elle dans cette direction?
NB: les 2 sont des puissances
Je veux trouver la question (a) en passant par les gradient.
En effet un théorème dit que la valeur maximale de la dérivée dans une direction est égale a la valeur absolue du gradient et elle est atteinte dans la direction du vecteur gradient. Ennutilisant ce théorème j'aurais plutot la direction pour augmenter la température le plus rapidement possible.
Que dois-je faire?
Gradient
7 messages
- Page 1 sur 1
Bonjour,
il suffit d'utiliser les différentielles sans doute avec un) et de trouver la ou les directions
et de trouver la ou les directions 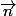
telle que.\vec{n}=0) qui vont annuler
qui vont annuler
la partie linéaire.
je crois me rappeler d'une formule:
le nombre dérivé de la fonction de R dans R:
)
est donnée par.\vec{n})
Comment doit on comprendre tes notations :
 := e^{ -x^2-2y^2-3z^2}) ?
?
est-ce bien cela ?
cordialement,
il suffit d'utiliser les différentielles sans doute avec un
telle que
la partie linéaire.
je crois me rappeler d'une formule:
le nombre dérivé de la fonction de R dans R:
est donnée par
Comment doit on comprendre tes notations :
est-ce bien cela ?
cordialement,
il me semble (sous toute réserve)
dans le développement limité:
=)
+)
n_{1}+\frac{\partial f}{\partial{y}}(x_{0},y_{0},z_{0})n_{2}+\frac{ \partial{f}}{\partial{z}}(x_{0},y_{0},z_{0})n_{3} \right)+)
)
application numérique:
=e^{-6})
nombre dérivé dans la direction (h,k,l):
(h,k,l)=(-2h-4k-6l)e^{-6}) (partie linéaire)
(partie linéaire)
nombre dérivé seconde divisé par :
:
e^{-6})
ça ce sont les coeff du développement limité de la fonction
d'une variable:
)
ensuite, je ne sais pas. Sans doute faut il maximiser le nombre dérivé,
j'en sais rien, et étudier la forme bilinéaire qui donne le nombre dérivé seconde
pour déterminer les directions vont donner un nombre dérivé seconde strictement négatif ? :hum:
dans le développement limité:
application numérique:
nombre dérivé dans la direction (h,k,l):
nombre dérivé seconde divisé par
ça ce sont les coeff du développement limité de la fonction
d'une variable:
ensuite, je ne sais pas. Sans doute faut il maximiser le nombre dérivé,
j'en sais rien, et étudier la forme bilinéaire qui donne le nombre dérivé seconde
pour déterminer les directions vont donner un nombre dérivé seconde strictement négatif ? :hum:
je suis allé regarder le principe du gradient sur Wiki.
On a les choses suivantes:
la différentielle de f s'exprime par:
-f(X_{0})=df. \left( \vec{X}-\vec{X_{0} \right))
où X est un vecteur de
La différentielle s'exprime comme un produit scalaire
et d'après l'inégalité de schwartz

la différentielle est maximale dans la direction du gradient.
la direction qui maximise la différentielle est donc:
)
soit la direction donnée par:
=\left( -2,-4,-6 \right))
2)
la vitesse de baisse de température est donnée par:
=(\phi)'(t) df.\vec{n})
si le mouvement est \vec{n})
soit
On a les choses suivantes:
la différentielle de f s'exprime par:
où X est un vecteur de
La différentielle s'exprime comme un produit scalaire
et d'après l'inégalité de schwartz
la différentielle est maximale dans la direction du gradient.
la direction qui maximise la différentielle est donc:
soit la direction donnée par:
2)
la vitesse de baisse de température est donnée par:
si le mouvement est
soit
j'ai réussi le (a)
Salut,
j'ai réussi a faire le (a)
mais je ne trouve pas la même chose que toi. Je trouve plutôt une direction dans le sens opposé 2i + 4j + 6K
En effet on demande la direction pour une baisse de le température rapide et non le contraire.
Par ailleur je ne comprend pas ton raisonement pour le calcul de la vitesse
j'ai réussi a faire le (a)
mais je ne trouve pas la même chose que toi. Je trouve plutôt une direction dans le sens opposé 2i + 4j + 6K
En effet on demande la direction pour une baisse de le température rapide et non le contraire.
Par ailleur je ne comprend pas ton raisonement pour le calcul de la vitesse
bjr,
ce que l'on appelle direction en maths, c'est une droite et non une demi droite.
j'ai fait le raisonnement suivant:
soit)
l'équation cinématique du mouvement
est \vec{n})
pour une certaine fonction vérifiant:
vérifiant:
=0)
 dérivable
dérivable
'(t)| = e^8)
ensuite on calcule la dérivée de:
 \vec{n}))
par la différentielle:
'(t) df.\vec{n}=(\phi)'(t) grad (f).\vec{n})
et la valeur absolue de la dérivée donne la vitesse
de la température.
ce que l'on appelle direction en maths, c'est une droite et non une demi droite.
j'ai fait le raisonnement suivant:
soit
l'équation cinématique du mouvement
est
pour une certaine fonction
ensuite on calcule la dérivée de:
par la différentielle:
et la valeur absolue de la dérivée donne la vitesse
de la température.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
