Equation trigo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nuklearis
- Membre Naturel
- Messages: 19
- Enregistré le: 15 Sep 2007, 10:38
-
 par Nuklearis » 06 Oct 2007, 10:05
par Nuklearis » 06 Oct 2007, 10:05
Bonjour
comment faire pour résoudre (racine(2)-1)cos x + sin x - 1 = 0 ?
merci
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 06 Oct 2007, 10:14
par yos » 06 Oct 2007, 10:14
Bonjour.
De façon générale , pour résoudre acos x+b sin x=c, on divise les deux membres par
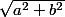
et on est ramené à
cos t cos x+sin t sin x= d où t est connu.
-
Nuklearis
- Membre Naturel
- Messages: 19
- Enregistré le: 15 Sep 2007, 10:38
-
 par Nuklearis » 06 Oct 2007, 17:39
par Nuklearis » 06 Oct 2007, 17:39
Ce qui après donne cos ( t - x )
merci je vais essayer
-
Nuklearis
- Membre Naturel
- Messages: 19
- Enregistré le: 15 Sep 2007, 10:38
-
 par Nuklearis » 07 Oct 2007, 07:52
par Nuklearis » 07 Oct 2007, 07:52
Désolé je ne vois vraiment pas comment on arrive a cos t cos x + sin t sin x...
je trouve cosx + sinx - 1 = 0
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Oct 2007, 08:16
par yos » 07 Oct 2007, 08:16
Après division des deux membres par \sqrt{a^2+b^2} , tu as un truc du genre ucosx+vsinx=d avec u²+v²=1, ce qui permet de dire qu'il existe un réel t tel que cost=u et sint=v.
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 07 Oct 2007, 09:52
par fibonacci » 07 Oct 2007, 09:52
Bonjour;
= \sqrt {a^2 + b^2 }( \frac{a}{{\sqrt {a^2 + b^2 } }}\cos x + \frac{b}{{\sqrt {a^2 + b^2 } }}sin x))
on pose
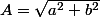
soit
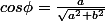
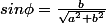
alors f(x)=
)
d'où
=Acos(x-\phi))
l'équation est équivalente à
=\frac{c}{A})
remarque
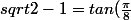)
-
Nuklearis
- Membre Naturel
- Messages: 19
- Enregistré le: 15 Sep 2007, 10:38
-
 par Nuklearis » 07 Oct 2007, 12:38
par Nuklearis » 07 Oct 2007, 12:38
C'est quoi phi ?
De plus je ne comprends pas comment tu passes de A = \sqrt {a^2 + b^2} à cos\phi et sin\phi
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
