Topologie !
Bonjour, je récapitule
voilà l'énoncé:
Soit un espace vectoriel sur
un espace vectoriel sur  de dimension finie muni d'une norme
de dimension finie muni d'une norme 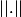 . Soit
. Soit  une partie non vide et bornée de
une partie non vide et bornée de  .
.
On définit=\sup \{||y-x||:\ x,y\in A\}) .
.
1) Montrer que si est bornée alors
est bornée alors 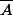 et
et ) sont bornés.
sont bornés.
2) Comparer) ,
, ) , et
, et ) lorsque
lorsque 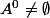 .
.
3) Montrer que)\leq diam(A)) .
.
4) Soient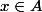 et
et 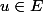 avec
avec 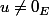 .
.
On considère l'ensemble .
.
Montrer que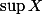 existe.
existe.
5) En déduire que toute demi-droite issue d'un point de
de  coupe
coupe ) .
.
6) En déduire que)=diam(A)) .
.
On a planté sur la question 3) et la question 6).
voilà l'énoncé:
Soit
On définit
1) Montrer que si
2) Comparer
3) Montrer que
4) Soient
On considère l'ensemble
Montrer que
5) En déduire que toute demi-droite issue d'un point
6) En déduire que
On a planté sur la question 3) et la question 6).
diam ( A ) = diam (Abarre)
on a clairement une inégalité
pour l'autre
pour epsilon >0
pour x et y dans A barre
il existe x ' et y ' dans A tels que
||x-x'|| < epsilon/2 et ||y-y'||
donc || x-y|| =< || x-x'|| +|| x' -y' || +|| y'-y||
donc || x-y|| < epsilon + diam (A)
valable pour tous x et y donc en passant au sup
diam( A barre) =< diam(A) +epsilon
donc diam(Abarre)=< diam (A)
le 3) en découle
on a clairement une inégalité
pour l'autre
pour epsilon >0
pour x et y dans A barre
il existe x ' et y ' dans A tels que
||x-x'|| < epsilon/2 et ||y-y'||
donc || x-y|| =< || x-x'|| +|| x' -y' || +|| y'-y||
donc || x-y|| < epsilon + diam (A)
valable pour tous x et y donc en passant au sup
diam( A barre) =< diam(A) +epsilon
donc diam(Abarre)=< diam (A)
le 3) en découle
ok alors pour la question 6), je crois que je peux procéder comme ça:
Soient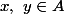 . On veut montrer qu'il existe
. On veut montrer qu'il existe ) tels que
tels que 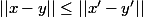 .
.
Si , c'est immédiat.
, c'est immédiat.
Si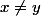 , on pose
, on pose 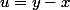 .
.
La demi-droite issue de et de vecteur directeur
et de vecteur directeur  coupe d'après 5) la frontière de
coupe d'après 5) la frontière de  .
.
On considère l'ensemble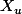 définit dans 4) associé cette demi-droite.
définit dans 4) associé cette demi-droite.
Notons la borne supérieure de
la borne supérieure de 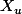 .
.
On a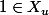 , car
, car 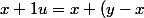=y\in A) .
.
Donc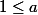 . D'autre part
. D'autre part ) , étant donné la résolution de la question 5).
, étant donné la résolution de la question 5).
La demi-droite issue de et de vecteur directeur -
et de vecteur directeur - coupe d'après 5) la frontière de
coupe d'après 5) la frontière de  .
.
On considère l'ensemble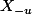 définit dans 4) associé cette demi-droite. Notons
définit dans 4) associé cette demi-droite. Notons  la borne supérieure de
la borne supérieure de 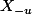 . D'autre part
. D'autre part ) .
.
On a alors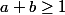 , d'où
, d'où
-(x-bu)|| = ||(a+b)u|| = (a+b)||u||\geq ||u|| = ||x-y||) .
.
Donc)\geq diam(A)) .
.
Soient
Si
Si
La demi-droite issue de
On considère l'ensemble
Notons
On a
Donc
La demi-droite issue de
On considère l'ensemble
On a alors
Donc
Bonjour :
Soit .
.
Définition $) :
:
 est continue sur
est continue sur  si et seulement si
si et seulement si  est continue en chacuns des points
est continue en chacuns des points 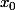 de
de  .
.
 est continue en
est continue en 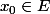 si et seulement si :
si et seulement si : ) \hspace{10cm} \exists U \in \upsilon(x) \hspace{10cm} : \hspace{10cm} f(U) \subset V $)
Question :
Montrer , uniquement à l'aide de la définition çi-dessus, que :
 est continue sur
est continue sur  si et seulement si
si et seulement si 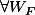 ouvert de
ouvert de  :
:  $) est un ouvert de
est un ouvert de  .
.
Merci infiniment !!
Soit
Définition
Question :
Montrer , uniquement à l'aide de la définition çi-dessus, que :
Merci infiniment !!
Bonsoir :
J'ai lu dans un cours de "geometrie differentielle" que :
Un ouvert non vide de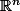 n'est pas homeomorphe à un ouvert non vide de
n'est pas homeomorphe à un ouvert non vide de 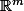 si
si 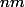 .
.
Pouvez vous m'expliquer pourquoi ?
C'est juste par curiosité que je lis ce cours là,... il ne fait pas partie du programme scolaire de cette année..! En plus, je l'ai jamais étudié !! voilà .. !
Merci d'avance !!
J'ai lu dans un cours de "geometrie differentielle" que :
Un ouvert non vide de
Pouvez vous m'expliquer pourquoi ?
C'est juste par curiosité que je lis ce cours là,... il ne fait pas partie du programme scolaire de cette année..! En plus, je l'ai jamais étudié !! voilà .. !
Merci d'avance !!
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
