Spe maths congruences

[J-R]

Bonsoir,

n un entier naturel.

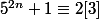
1) démontrer que ca c'est fait

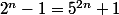
2) en déduire que l'équation n'admet pas de solutions dans

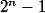
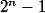
là je blocque: mon idée serait de démontrer que ne s'écrit jamais sous la forme 3k+2 soit démontrer que n''est pas congru à 2 modulo 3 mais j'ai du mal.

de plus dans la première question je l'ai montrer pour tout entier naturel n mais dans la 2) il demande les solutions dans donc je suis un peu embrouillé....

merci

[rene38]

Bonsoir



Sachant que on a donc

autrement dit, est multiple de 3

Or ...

[lapras]

Salut,
autre idée :
remarque que 2 = -1 [3]
donc
2^n = (-1)^n (3)
donc
2^n -1 = 0 (3)
si n pair
ou
2^n-1 = -2 (3) = 1(3)

donc pour tout n, 2^n-1 jamais = 2 [3]
déduis en le résultat :)

[J-R]

lapras: oui j'avais fait cette méthode suivant la parité de n mais là on a prouvé qu'il n'y avait pas de solutions dans N non ?

rene38: ouias donc il faut que je prouve que 2^n n'est jamais multiple de 3...

merci

[lapras]

J-R, même avec notre méthode ca prouve qu'il n'ya pas de solutions !
Si deux nombres sont égaux, alors ils ont le même reste par la division euclidienne par 3 donc si a=b, alors a congrue à b mod (3)
c'est la définition du modulo

or la ils n'ont jamais les mêmes restes : il n'y a pas de solutions

[rene38]

rene38: ouias donc il faut que je prouve que 2^n n'est jamais multiple de 3...

Aux dernières nouvelles, les seuls diviseurs (autres que 1) de 2^n sont les 2^k, k naturel, 1<=k<=n.

[Maeredhel]

pour la forme tu peux meme enlever ton "autres que 1" et mettre 0<=k<=n
mais bon, je pinaille :D