Fonction tangente

[S@m]

Bon ben on se fait un ptit dialogue a deux là...Tout ca pour dire que c'est le signe de la difference de la fonction tangente et de de sa tangente en O et non le signe de la difference de la fonction tangente et de son asymptote...mais on a le droit de le faire quand meme pas vrai? Help? Sos? lool :briques:

[julian]

Bon j'ai réussi mais sans justification... :marteau: :briques:

[S@m]

Je viens de trouver(Edit: heu en fait JE viens pas de trouver, thanks Alphaminou :fr: ), je te le transmet par Mp jul'...juste un dernier truc pour les ames perdu qui oseraient nous aider ici lol...Escque si on demande de prouver que la fonction tangente est invariante de vecteur 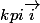et qu'on prouver qu'elle est invariante pour toute translation de vecteur 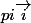c'est bon?
De meme si on demande de prouver qu'un point (kpi;o) est centre de symetrie et qu'on le prouve pour (pi;o) escque c'est bon (ave cun minimum de justification) :marteau: ?

[julian]

S@m tu me désepères...une élève de ton niveau ne devrait pas se permettre de demander de telles choses! :ptdr:
Maintenant que le dm a été rendu çà ne va pas servir à grnd chose que je te dises ce que j'ai fait,mais je vais le mettre quand même :id:
1èrement: si la une fonction est périodique de période ,elel est également périodique de période 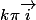,avec k \in \mathbb{Z}.Donc si elle est invariante de vecteur ,elle sera aussi invariante de vecteur.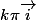

Ensuite:pour ta 2è question,je suppose que tu veux parler de la formules où il fallait prouver que était bien un centre de symétrie de la courbe représentative de la fonction tangente:
je suis passé de: à en justifiant que c'était parce que la fonction tangente était périodique de période
:++:
ps:réédites ton message encore et mets \pi entre les balises TEX et non pi. :id:

[S@m]

Lool t'es vraiment bete julian...je t'ai dit ce que j'avais fait par oral, et tu te rends bien compte que c'est exactement pareil! :ptdr:
Bref, le sujet est clos on a rendu le DM :stupid_in
Merci a tous pour votre aide, on va reprendre notre grade de "petite liçeen(e) tentant d'aider les moins petit(e)s... :marteau: "