Du cour..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 30 Sep 2007, 12:17
par sue » 30 Sep 2007, 12:17
Bonjour,
j'ai quelques questions du cour ..
1- a-t-on
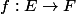
injective
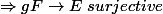
?
2- je ne comprends pas une preuve dans mon cour !
on veut ontrer par
reccurence que :

pas de prob pour l'initialisation .
sinon voilà la suite :
soit

on suppose que
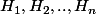
sont vraies et mq
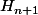
l'est aussi .
-
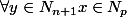
tq
)
, ie f est surj et f inj dc f est bij .
- sinon
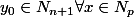
:
)
.
on considère
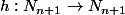
tq
=n+1)
et
=y_0)
et
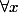
différent de
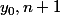
=x)
, dc h bij ie surj .
on pose
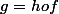
on a donc g inj
"on a
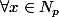
,
\neq n+1)
( à partir de là je suis perdue :hein: )
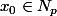
tq
=n+1)
)=n+1 \Rightarrow f(x_0)=h(n+1)=y_0)
on note
=g(x))
on a g' inj
finalement

"
je ne comprends pas bien le raisonnement !!
Merci
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 30 Sep 2007, 12:49
par sue » 30 Sep 2007, 12:49
d'accord ! merci Rain' .
sinon t'as eu une idée sur ce qu'on a fait à la fin de la preuve ?
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 30 Sep 2007, 16:13
par sue » 30 Sep 2007, 16:13
biensûr , désolée !
-
pianozik
- Membre Relatif
- Messages: 201
- Enregistré le: 18 Juin 2005, 11:50
-
 par pianozik » 30 Sep 2007, 17:15
par pianozik » 30 Sep 2007, 17:15
c'est ce que j'avais remarqué:++:
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 30 Sep 2007, 18:03
par sue » 30 Sep 2007, 18:03
Ok , j'ai trouvé une autre dém' plus claire .
mais sinon j'ai une autre question apparemment simple mais je vois rien pr le moment .
je cheche à déteriner cet ensemble :
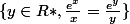
-
pianozik
- Membre Relatif
- Messages: 201
- Enregistré le: 18 Juin 2005, 11:50
-
 par pianozik » 30 Sep 2007, 21:12
par pianozik » 30 Sep 2007, 21:12
alors on a


donc

dans ce cas serait différente de n+1 (puisque

est une bijection et l'image de

c'est

)
et comme

est une bijection, alors il existe un antécédant de

que vous avez noté

donc

.
Or

est bijective et si tu remarques tu vas trouver que

. Donc

.
Ce qui vient après je crois que c'est simple.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 30 Sep 2007, 22:14
par fahr451 » 30 Sep 2007, 22:14
sue a écrit:Ok , j'ai trouvé une autre dém' plus claire .
mais sinon j'ai une autre question apparemment simple mais je vois rien pr le moment .
je cheche à déteriner cet ensemble :
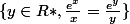
bonsoir
x est fixé donné je présume
étudie les variations de f , f(y)= exp (y) /y et discute suivant x le nombre de solutions c'est tout ce qu'on peut raisonnablement faire
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 30 Sep 2007, 22:42
par sue » 30 Sep 2007, 22:42
effectivement , je fatigue :brique:
ais sinon , merci pianozik celà e cofire ce que j'ai mais c'est ç
-
pianozik
- Membre Relatif
- Messages: 201
- Enregistré le: 18 Juin 2005, 11:50
-
 par pianozik » 30 Sep 2007, 23:37
par pianozik » 30 Sep 2007, 23:37
Je crois qu'il faut fixer

et étudier la fonction

.
Je l'ai représentée et j'ai trouvé que

Donc pour

. On varie

de telle sorte qu'on ait une fonction constante de valeur

. Et donc on a l'égalité lorsqu'on a intersection de ces deux courbes, donc pour


. Je n'en suis pas sûr ... donc si quelqu'un a des remarques qu'il les fasse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités


 donc
donc  dans ce cas serait différente de n+1 (puisque
dans ce cas serait différente de n+1 (puisque  est une bijection et l'image de
est une bijection et l'image de  c'est
c'est  )
) est une bijection, alors il existe un antécédant de
est une bijection, alors il existe un antécédant de 
 .
. est bijective et si tu remarques tu vas trouver que
est bijective et si tu remarques tu vas trouver que  . Donc
. Donc  .
. et étudier la fonction
et étudier la fonction  .
.
 . On varie
. On varie  . Et donc on a l'égalité lorsqu'on a intersection de ces deux courbes, donc pour
. Et donc on a l'égalité lorsqu'on a intersection de ces deux courbes, donc pour  . Je n'en suis pas sûr ... donc si quelqu'un a des remarques qu'il les fasse.
. Je n'en suis pas sûr ... donc si quelqu'un a des remarques qu'il les fasse.