Probleme de maths
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Daedin
- Messages: 4
- Enregistré le: 30 Sep 2007, 17:25
-
 par Daedin » 30 Sep 2007, 17:28
par Daedin » 30 Sep 2007, 17:28
Bonjour,
Voila j'ai un probleme que je n'arrive pas a resoudre pouvez vous m'aidez?
Demontrer que le produit de quatre entiers naturels consequitifs augmenté de 1 est le carré d'un entier naturel.
Merci d'avance :)
-
eejit
- Membre Relatif
- Messages: 236
- Enregistré le: 08 Mai 2007, 08:52
-
 par eejit » 30 Sep 2007, 17:36
par eejit » 30 Sep 2007, 17:36
C'est pas la première fois qu'il passe ce sujet là.
Soit n un entier naturel, comment peux-tu écrire l'énoncé?
-
Daedin
- Messages: 4
- Enregistré le: 30 Sep 2007, 17:25
-
 par Daedin » 30 Sep 2007, 17:50
par Daedin » 30 Sep 2007, 17:50
x (x+1) (x+2) (x+3) = n²
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 30 Sep 2007, 17:53
par Imod » 30 Sep 2007, 17:53
eejit a écrit:C'est pas la première fois qu'il passe ce sujet là.
En effet et sans indice ce n'est pas évident . En notant
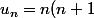(n+2)(n+3)+1)
et
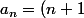(n+2))
alors
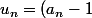^2)
.
Imod
-
eejit
- Membre Relatif
- Messages: 236
- Enregistré le: 08 Mai 2007, 08:52
-
 par eejit » 30 Sep 2007, 17:59
par eejit » 30 Sep 2007, 17:59
Daedin a écrit:x (x+1) (x+2) (x+3) = n²
C'est pas ça... le produit augmenté de 1 d'où: x (x+1) (x+2) (x+3)
+1.
Après, il ne reste qu'à développer l'expression.
-
Daedin
- Messages: 4
- Enregistré le: 30 Sep 2007, 17:25
-
 par Daedin » 30 Sep 2007, 18:09
par Daedin » 30 Sep 2007, 18:09
En dévelopant l'equation je trouve x^4+5x^3+7x^2+5x+7
Je ne voit vraiment pas de solution a ce probleme...
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 30 Sep 2007, 18:13
par Imod » 30 Sep 2007, 18:13
En utilisant les notations déjà données , montre que
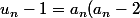)
, la suite est facile !
Imod
-
eejit
- Membre Relatif
- Messages: 236
- Enregistré le: 08 Mai 2007, 08:52
-
 par eejit » 30 Sep 2007, 18:16
par eejit » 30 Sep 2007, 18:16
Ton développement est faux.
-
Daedin
- Messages: 4
- Enregistré le: 30 Sep 2007, 17:25
-
 par Daedin » 30 Sep 2007, 18:32
par Daedin » 30 Sep 2007, 18:32
Je seche, je ne comprend pas comment demontrer.
Le probleme c'est que je ne sait pas ce que l'on cherche a vrai dire
De plus je ne comprend pas comment a partir de l'equation je peut trouver:
Un= (An-1^)²
-
eejit
- Membre Relatif
- Messages: 236
- Enregistré le: 08 Mai 2007, 08:52
-
 par eejit » 30 Sep 2007, 18:35
par eejit » 30 Sep 2007, 18:35
redéveloppe l'expression.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
