Ens. finis

[sue]

bonsoir,

je cherche la preuve d'une proposition assez intuitive :

"il existe une surjection de {1....n}sur{1...p} ssi "

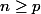
reccurence ?

merci

[SimonB]

Un sens est évident.

Pour l'autre, il suffit de remarquer que tu as au plus n images distinctes ; si , il y a donc des points non atteints. Pas la peine de faire des récurrences pour ce genre de choses !

[emdro]

Bonsoir,

comme (puisqu'une fonction associe au plus une image), c'est réglé!

[sue]

D'accord :briques:

je vous remercie

[Yipee]

Bonsoir,

comme (puisqu'une fonction associe au plus une image), c'est réglé!

Comme je l'ai déjà écrit dans un autre post, je ne pense pas que cette méthode soit la bonne. La raison est que la proposition que l'on veut démontrer sert à définir par la suite la notion de cardinal d'un ensemble fini. On ne peut donc pas s'en servir dans la démonstration.

[emdro]

Remarque intéressante. Effectivement, il est toujours intéressant de se poser la question des prérequis, afin de ne pas tourner en rond.

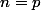
Dans ce cas, si la relation est définie par "Il existe une bijection de sur ", la relation est définie par "Il existe une surjection de sur ", non? Auquel cas, c'est encore plus facile...