Question topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
 par ClaireD » 23 Sep 2007, 15:51
par ClaireD » 23 Sep 2007, 15:51
Bonjour,
je suis étudiante en 3ème année de maths et je me pose une question :
soit f une fonction bornée sur [a,b].
soit E l'ensemble de ses points de discontinuités.
w(f,x)= inf delta>0 { sup(f(y)) - inf(f(y)),ydans[a,b] : |x-y|
on appelle w(f,x) l'oscillation de f en x dans [a,b]
on veut montrer que pour §>0 E§ = { x tel que w(f,x) >= § } est un fermé.
j'avais pensé à utiliser le théorème : "toute image reciproque d'un fermé par une fonction continue f est un fermé"
Seulement je n'arrive pas à montrer que w est continue...c'est cela qui me gène...c'est surement tout bete.... je dois trop me compliquer
Si vous avez des suggestions n'hesitez pas
Merci,
Claire.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Sep 2007, 17:04
par barbu23 » 23 Sep 2007, 17:04
Bonjour:
On a :
 = \displaystyle \inf_{\hspace{10cm} \delta > 0 \\ y \in [a,b] } \{ \hspace{10cm} \sup(f(y)) - \inf(f(y)) \hspace{10cm} / \hspace{10cm} \| x-y \| 0 $)
:
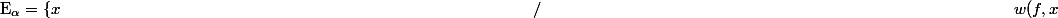 > \alpha \} $)
est un fermé .
Oui, on peut poser :
 = \displaystyle \inf_{\hspace{10cm} \delta > 0 \\ y \in [a,b] } \{ \hspace{10cm} \sup(f(y)) - \inf(f(y)) \hspace{10cm} / \hspace{10cm} \| x-y \| < \delta \} $)

c'est quoi c'est

?
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
 par ClaireD » 24 Sep 2007, 15:51
par ClaireD » 24 Sep 2007, 15:51
[quote="barbu23"]Bonjour:
On a :
 = \displaystyle \inf_{\hspace{10cm} \delta > 0 \\ y \in [a,b] } \{ \hspace{10cm} \sup(f(y)) - \inf(f(y)) \hspace{10cm} / \hspace{10cm} \| x-y \| 0 $)
:
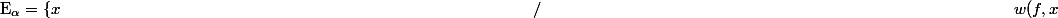 > \alpha \} $)
est un fermé .
Oui, on peut poser :
[TEX]$\ w \hspace{10cm} : \hspace{10cm} x \longrightarrow w(f,x) = \displaystyle \inf_{\hspace{10cm} \delta > 0 \\ y \in [a,b] } \{ \hspace{10cm} \sup(f(y)) - \inf(f(y)) \hspace{10cm} / \hspace{10cm} \| x-y \| 0} meme si l'on ne sait pas si f est continue, peut-on tout de meme montrer que x->w(f,x) est continue ?....sinon j'ai pensé à prouver que E§ est fermé avec la caractérisation des suites mais c'est plus long et plus compliqué....
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Sep 2007, 17:36
par yos » 24 Sep 2007, 17:36
Je pense pas que
)
soit continue. Imagine une fonction f avec un seul point de discontinuité a, tu as
 \neq 0)
et
=0)
pour
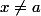
.
Une preuve directe s'impose ici.
 par legeniedesalpages » 24 Sep 2007, 23:31
par legeniedesalpages » 24 Sep 2007, 23:31
Bonsoir,
on peut peut-être montrer que toute suite convergente
)
de points de

a sa limite dans

.
A voir. :hein:
-
ClaireD
- Membre Naturel
- Messages: 22
- Enregistré le: 22 Sep 2007, 14:12
-
 par ClaireD » 25 Sep 2007, 02:08
par ClaireD » 25 Sep 2007, 02:08
effectivement , j'ai rédigé une réponse en essayant de montrer que toute suite convergente de E$ converge dans E$....mais disons que c'est plus difficile à écrire correctement les choses de cette manière...
En tout cas merci pour vos suggestions
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 25 Sep 2007, 13:31
par yos » 25 Sep 2007, 13:31
C'est pas très dur.
Soit

et
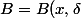)
.
B rencontre

en

. Soit
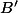
une boule de centre

contenue dans

. Par définition de
)
, on a
-\inf_{t\in B'} f(t)|\geq\epsilon)
donc a fortiori
-\inf_{t\in B} f(t)|\geq\epsilon)
.
Et comme c'est vrai pour toute boule B contenant x, ça reste vrai en passant à l'inf sur ces boules :
\geq \epsilon)
et donc

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
