Nilpotence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 29 Avr 2007, 15:55
par Pythix » 29 Avr 2007, 15:55
Bonjour,
on considère des matrices dans Mn(R) :
Comment montrer que si A et B sont deux matrices nilpotentes qui commutent, pour tout réel x on a :
A+xB nilpotente ? et que si p et q sont deux entiers tels que p+q>n alors
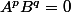
?
merci d'avance
je me doute qu'il faut utiliser le binôme mais je vois pas trop...
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 29 Avr 2007, 16:02
par Pythix » 29 Avr 2007, 16:02
euh :
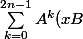^{2n-1-k})
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 29 Avr 2007, 16:05
par Pythix » 29 Avr 2007, 16:05
je ne savais pas comment faire les coefficients...
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 29 Avr 2007, 16:57
par Pythix » 29 Avr 2007, 16:57
pour montrer qu'une matrice strictement triangulaire est nilpotente :
peut on faire une récurrence sur n, le nombre de lignes et de colonnes ?
je ne sais pas si ma récurrence tient la route:
je suppose qu'il existe p tel que pour une matrice A de Mn(R) A^p=0
pour l'hérédité je prends une matrice B de
)
, je l'élève au carré et je dis que l'on se ramène à l'hypotèse de récurrence...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 30 Avr 2007, 17:09
par yos » 30 Avr 2007, 17:09
Je fais remonter car je vois que personne n'a évoqué la deuxième question qui est intéressante.
A+xB nilpotente donc
^n=0)
, donc
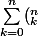A^{n-k}B^kx^k=0)
. Voilà donc un polynôme en x à coefs dans
)
, identiquement nul.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 05 Mai 2007, 08:47
par yos » 05 Mai 2007, 08:47
Il y a le résultat classique suivant :
"Si
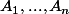
sont nilpotentes et commutent deux à deux alors leur produit est nul."
Je sais le prouver, mais je me demandais si on pouvait le déduire du résultat précédent.
-
Jonathan_
- Membre Naturel
- Messages: 41
- Enregistré le: 16 Déc 2006, 19:37
-
 par Jonathan_ » 23 Sep 2007, 07:07
par Jonathan_ » 23 Sep 2007, 07:07
Bonjour... Est ce que quelqu'un a une idée pour montrer une réciproque (partielle) de la première question?? je m'explique... il faut montrer que en prenant A et B dans Mn(C) tel que M=A+xB avec M nilpotente pour (n+1) valeurs de x alors on a A et B nilpotentes... j'ai essaye de développer avec le binôme, pour essayer de me ramener a un polynome en B ou en A pour peut être raisonner sur les racines du polynômes mais c'était une mauvaise idée, et à part sa je vois pas trop...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 23 Sep 2007, 10:07
par fahr451 » 23 Sep 2007, 10:07
notons x0,...,xn n+1 ces valeurs
pour i = 0,...,n
on a [A+Bx(i) ]^n = 0
en développant on obtient
sigma k = 0,...,n c(k) x(i)^k = 0
avec c(k) = (k parmi n ) A^(n-k) B^k
est un système n+1, n+1 d'inconnues les c(k) de matrice de van der monde des x(i) , de cramer donc l'unique solution est
pour tout k
c(k) = 0
en particulier c(0) = A^n = 0
et c(n) = B^n = 0
-
Jonathan_
- Membre Naturel
- Messages: 41
- Enregistré le: 16 Déc 2006, 19:37
-
 par Jonathan_ » 23 Sep 2007, 10:11
par Jonathan_ » 23 Sep 2007, 10:11
Ok, merci beaucoup, j'avais pas pensé a poser c(k)...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
