Aide factorisation

par **neo765** » 10 Sep 2005, 21:17

Je bute sur cette factorisation :
8x² - 14x + (49 - 16x²)

Si j'ai trouvé avant que vous me répondez je posterai

Merci

par **S@m** » 10 Sep 2005, 21:23

Tu sais comment factorisez un trinome du second degré?

par **Aldebaran** » 10 Sep 2005, 21:51

neo765 a écrit:Je bute sur cette factorisation :
8x² - 14x + (49 - 16x²)

Pour la première partie, (celle qui n'est pas entre parenthèses), il y a un facteur commun qui est évident :

et

sont tous deux des multiples de

...

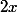
Pour l'expression qui est entre parenthèses, rappelle toi les formules des identités remarquables que tu as dut voir en troisième (vu que je suppose que tu est en seconde !!!) : comment peut-on écrire autrement

. les nombres

et

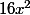
sont-ils les carrés d'autres nombres ?

par **S@m** » 10 Sep 2005, 22:00

S'il connait les trinomes, il peut egalement factorisé a l'aide des deux racines reels du trinome... :happy2:

par **neo765** » 10 Sep 2005, 23:07

Je ne connais pas les notions de trinôme

par **neo765** » 10 Sep 2005, 23:10

Je trouve ça :
(4x - 7)(6x + 7)

Pouvais vous me dire si c'est bon ?

par **Anonyme** » 10 Sep 2005, 23:15

Aldebaran a écrit:Pour la première partie, (celle qui n'est pas entre parenthèses), il y a un facteur commun qui est évident : et sont tous deux des multiples de ...

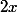
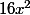
Pour l'expression qui est entre parenthèses, rappelle toi les formules des identités remarquables que tu as dut voir en troisième (vu que je suppose que tu est en seconde !!!) : comment peut-on écrire autrement . les nombres et sont-ils les carrés d'autres nombres ?

Il manque une valeur absolue dans ta signature chef :lol3:

par **S@m** » 11 Sep 2005, 10:31

Pour savoir si c'est bon, il te suffit de redevelopper :happy2:

par **neo765** » 11 Sep 2005, 11:36

Non, c'est pas bon :cry:

J'ai fait ça :

2x(4x - 7) + (7 - 4x)(7 + 4x)
(4x - 7)[(2x + (7 + 4x)]
(4x - 7)(2x + 7 + 4x)
(4x - 7)(6x + 7)

Mais c'est pas bon :cry:

Merci

par **Clain** » 11 Sep 2005, 12:44

Salut,
La première factorisation est juste :
8x² - 14x + (49 - 16x²) = 2x(4x - 7) + (7 - 4x)(7 + 4x)

L'erreur est dans le signe de la ligne suivante :
(7 - 4x) = - (4x - 7)

ça change un signe dans tes crochets !

par **neo765** » 11 Sep 2005, 14:22

Je ne comprend pas où est mon erreur !

par **Anonyme** » 11 Sep 2005, 14:27

Bonjour,

Je débarque et je regarde cet exercice mais il y a un truc que je ne comprends pas (j'ai tjs eu qq soucis avec la factorisation).
Comment passe t'on de la première à la deuxième ligne ?

2x(4x - 7) + (7 - 4x)(7 + 4x)
(4x - 7)[(2x + (7 + 4x)]

Voilà merci pour la réponse

par **neo765** » 11 Sep 2005, 14:42

J'ai trouvé la bonne réponse ! Merci

Bonne résolution :

= 8x² - 14x + (49 - 16x²)
= 2x(4x - 7) + (7 - 4x)(4x + 7)
= 2x(4x - 7) - (4x - 7)(4x + 7)
= (4x - 7)[(2x - 4x - 7)]
= (4x - 7)(-2x - 7)

Voilà merci

par **Anonyme** » 11 Sep 2005, 14:45

Bah moi je comprends toujours pas...

Aide factorisation

Aide factorisation

Qui est en ligne