Probleme une petite aide svp
18 messages
- Page 1 sur 1
Probleme une petite aide svp
Bonjour
voila que depuis 9 h du mat je cherche la reponse pour mon dm j ai beau reflechir mais je trouve pas
voila le probleme
2 montrer que pour tout nombre n :
n(n+1)(n+2)(n+3)+1 = (n²+3n+1)²
indication on peut ecrire n(n+1)(n+2)(n+3) = [n(n+1)][(n+2)(n+3)] et n²+3n+1= n²+(3n+1)
voila je cherche je cherche c est un Dm pour lundi mais je trouve pas :cry: :cry:
alors aidez moi svp merci
voila que depuis 9 h du mat je cherche la reponse pour mon dm j ai beau reflechir mais je trouve pas
voila le probleme
2 montrer que pour tout nombre n :
n(n+1)(n+2)(n+3)+1 = (n²+3n+1)²
indication on peut ecrire n(n+1)(n+2)(n+3) = [n(n+1)][(n+2)(n+3)] et n²+3n+1= n²+(3n+1)
voila je cherche je cherche c est un Dm pour lundi mais je trouve pas :cry: :cry:
alors aidez moi svp merci
t'a remarqué ca j'imagine :
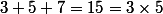
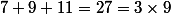
c'est 3fois celui du milieu
pour démonter
tu dis que n impaire => n=2k+1 tu prend les deux impaires suivants (facile en fonction de k), tu fait la sommes tu remarque que ca fait ? fois ? et voila
si t'a pas compris : ( ecrit en blanc donc selectionne avec la souris pour voir)
alors, on fait la sommes et puis :
2k+1 + 2k+3 + 2k+5= 6k+9=3(2k+3) = 3fois celui du milieu
c'est 3fois celui du milieu
pour démonter
tu dis que n impaire => n=2k+1 tu prend les deux impaires suivants (facile en fonction de k), tu fait la sommes tu remarque que ca fait ? fois ? et voila
si t'a pas compris : ( ecrit en blanc donc selectionne avec la souris pour voir)
alors, on fait la sommes et puis :
2k+1 + 2k+3 + 2k+5= 6k+9=3(2k+3) = 3fois celui du milieu
re voila vous savez le premier truc que je vous est demaindez
exercice 2
1calculer le nombre de 4 entier consecutifs et ajouter 1 que remarque ton ?
j ai trouver ca
2.a) c etsc elui que je vous ai demander au tout debut du topic
montrer que pour tout nombre n :
n(n+1)(n+2)(n+3)+1 = (n²+3n+1)²
indication on peut ecrire n(n+1)(n+2)(n+3) = [n(n+1)][(n+2)(n+3)] et n²+3n+1= n²+(3n+1)
3 expliquer le resulta trouver a la question 1
voila je cherche le 3
jai besoin de votre aide une fois de plus merci encore pour tout
exercice 2
1calculer le nombre de 4 entier consecutifs et ajouter 1 que remarque ton ?
j ai trouver ca
2.a) c etsc elui que je vous ai demander au tout debut du topic
montrer que pour tout nombre n :
n(n+1)(n+2)(n+3)+1 = (n²+3n+1)²
indication on peut ecrire n(n+1)(n+2)(n+3) = [n(n+1)][(n+2)(n+3)] et n²+3n+1= n²+(3n+1)
3 expliquer le resulta trouver a la question 1
voila je cherche le 3
jai besoin de votre aide une fois de plus merci encore pour tout
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
