Proba / Stats ...

[Guga78]

Bonjour à tous,

Voilà, j'ai 4 exercices de maths à réaliser pour des rattrapages.
Seulement, comme vous l'aurez deviné je suis légerment bloqué... pour ne pas dire complètement.
Je vous soumets le sujet :
Exercice 1 :
Sur une autoroute il circule 10% de camions et 90% de voitures.
1- Déterminer l’univers .
2 - On se place au bord de l’autoroute et on observe n véhicules. Quelle est la loi de la variable aléatoire donnant le nombre de camions observés ?

On note la variable aléatoire correspondant à la proportion de camions observés.
(Indication : peut s’écrire comme une somme de variables aléatoires indépendantes)

3- Calculer l’espérance et la variance .
4- Déterminer le nombre minimum de véhicules à observer pour que la proportion de camions soit située entre 8% et 12%, avec une probabilité supérieure à 96%.
a- En utilisant le théorème central limite.
b- En utilisant la loi faible des grands nombres.
5- Chaque jour 10000 véhicules circulent sur cette autoroute.
Peut-on approcher la loi de de la question 2 par la loi de poisson ? Si oui déterminé son paramètre.


Exercice 2:
Pour contrôler la qualité d’un lot de pièces, on en prélève un échantillon de taille
N = 5, et on constate que k’ = 3 pièces sont défectueuses.
On suppose que la population K obéit à une loi binomiale B( N , p )

1) Déterminer l’expression littérale de la fonction de vraisemblance L(k’;p), et tracer son allure en fonction de p. En quel point le maximum est-il atteint ?
2) Exprimer l’estimateur du maximum de vraisemblance du paramètre p. Cet estimateur est-il biaisé


Exercice 3:
Pour déterminer l’âge moyen de ses clients, une grande entreprise de confection pour hommes prélève un échantillon aléatoire de 50 clients et trouve une moyenne de 36 ans et une variance s2 =144.
1- Déterminer un intervalle de confiance au risque de 5% de la moyenne d’âge.
2-Supposer que pour le même risque d’erreur, on veuille réduire la longueur de
l’intervalle de façon précise, à 2ans.
Quelle doit être alors la taille de l’échantillon ?

3- Déterminer un intervalle de confiance au risque 5% pour l’écart type.


Exercice4 :
Une variable aléatoire suit la loi normale N(0,s). Au vu d’un échantillon indépendant (x1, x2, …, xn) de la loi de X, on veut choisir entre les hypothèses
H0 : s = 1
H1 : s = 2
1- On veut déterminer le test à effectuer par la méthode de Neyman et Pearson
a- Déterminer les fonctions de vraisemblance L(x1, …, xn, 0) et L(x1, …, xn, 1).
En déduire le rapport de vraisemblance , et
c- Déterminer la région critique C =
2- Pour suivant la loi normale N(0, ) , on admet que suit la loi de c2 à n degrés de libertés.
a- Pour n = 20 et le niveau a = 2.5% , déterminer la constante
de la région critique
b- Déterminer la puissance du test 1-b . La puissance du test est-elle
maximale?


Bien entendu je ne vous demande pas de les faire à ma place, mais de me donner des pistes. Je devrais en plus de les rendre les expliquer durant une demie heure. J'espère donc pouvoir y comprendre quelque chose.
Je vous remercie d'avance pour l'aide que vous pourrez m'apporter.

Alex.

[nuage]

Salut,

pour l'exercice 1 :
question 1 :
l'univers n'est pas défini, mais on peut penser, au vu de la question 2, qu'il s'agit de l'ensemble de n observations.

question 2 :
La réponse attendue est que cette v.a.(disons X) suit une loi binomiale. Ce qui suppose que la proba d'observer un camion au k-ième véhicule est indépendante des k observations précédentes. Ce n'est sans doute pas vrai en pratique, mais je crois que c'est la réponse attendue.

question 3 :
L'espérance et la variance de la proportion s'obtiennent à partir de celles de X.
Et pour X on trouve ça partout.


[modification]
C'est une mauvaise idée d'avoir mis les énoncés en code.
Ils sont pénibles à lire, chez moi du moIns.
Sur ce faut que j'y aille.

A+

[Guga78]

Bonjour nuage,

Je te remercie de tes eclaircissements.
Pour la question 1 ca donne donc un univers compris entre 0 et n?
Pour la question 2 tu me dit quelle est la probabilité d'observer un camion aprés k passage de véhicules. Or la réponse attendue serait plutot le nombre total de camion observé en fonction du nombre de véhicules. Je me trompe peut être.
Si j'ai bien compris tes pistes je dois calculer pour la question 2 la loi binomiale B(n; nbre de camions observés)?

En tout cas merci d'avoir pris un peu de temps pour m'éclairer :happy2:

Alex.

[nuage]

Salut,
Très rapidement : l'univers serait un ensemble de n observations de véhicules.
On peut aussi bien s'intéresser à la marque du véhicule, au premier chiffre de son immatriculation, à son pays d'immatriculation, etc...
Ceci étant les valeurs prises par la v.a. donnant le nombre de camion observés prend des valeurs entre entières 0 et n.
Pour la 2° question on s'intéresse au nombre de camions. Soit X la v.a. associant le nombre de camions observés à n observations consécutives.
La question est : Quelle est la loi de X. Si on admet que la proba d'observer un camion ne dépend pas des observations précédentes (et reste toujours égale à 10%) la loi de X est une loi binomiale de paramètres n et 0,1. Son espérance est et sa variance . Voir le cours pour plus de précisions. La proportion F de camions est une v.a. définie par F=X/n. Donc (voir le cours) E(F)=E(X)/n=0,1 et V(F)=V(X)/n²=0,09/n.

Pour la question 4.a :
Si n est assez grand F suit approximativement une loi normale d'espérance 0,1 et d'écart-type . Je te laisse terminer les calculs, demande si tu as besoin d'aide, mais n'attends pas de réponses avant demain soir.
Pour le 4.b. la loi faible des grands nombres donne une inégalité que je te laisse exploiter.

pour la question 5 l'approximation de la loi de X par une loi de Poisson est possible mais ne présente aucun intérêt : il vaut mieux l'approcher par une loi normale. Ce que l'on fait en général pour une loi de Poisson de paramètre 1000.


A+

[Guga78]

Merci beaucoup Nuage,

Je comprends beaucoup mieux le sujet ainsi.
Bonne soirée.

Alex.

[Guga78]

Salut !!

Juste une question pour ce qui est de la loi normale de la question 4a, en fait j'utilise la loi normale centrée reduite avec 0.8<=Yn<=0.12 et Yn(m=0.1; )
ou bien Yn(0;1)?

Merci d'avance.

[nuage]

Salut,
je suppose que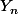 est la v.a. qui donne la proportion de camion observée.
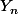suit (à peu près) la loi normale de paramètres et .
On veut déterminer la plus petite valeur de telle que :
.

Pour cela on considère la v.a. .
T suit la loi normale centrée réduite (espérance 0 , écart-type 1).

Ensuite on a :

En notant la fonction de répartition de la loi normale centrée réduite, la proba précédente est égale à

Il reste à résoudre


Pour ceci on utilise une table (ou une calculette plus performante que la mienne, ou un tableur...)
Sauf erreur de ma part on trouve .

A+

[Guga78]

Bonsoir,

Merci pour ton aide précieuse!!
Je me demande comment fais tu pour passer de 0.08-m à -0.02racine de n.
Je sais je suis une quiche en maths... :hum:
En tout cas merci du temps que tu m'accorde.

Alex.

Modif : Ok j'ai compris comment tu trouvais 0.02. D'aprés le tableau de la loi normal centrée réduite. en faisant pi(0.12) - pi(0.08)

Re-Modif : En revanche, je ne comprends pas comment tu fais pour passer de 0.02racine de n /0.3 à racine de n /15.

[nuage]

Je passe de à -0,02 car .
Ensuite

car et que .

A+ et ne te décourages pas.

[Guga78]

Merci et ca fait longtemps que je me serais découragé si tu ne m'avais pas éclairci dailleur ca commence même à m'interesser :we: malgré le fait que certaines parties restent obscures.

PS : C'est la table de la loi normale qu'on utilise pour la derniere partie de la 4 a pour trouver n?

[all]

Bonsoir, j'ai aussi ces exercices à faire :triste: et vu que je suis également mauvais en math...

Bref, pour moi l'univers se résume au deux évènement possible :
'voiture' et 'camion'.

Pour les questions 2 et 3 je suis d'accord

Là par contre j'ai pas compris comment on passe de la probabilité à la fonction de répartition

En notant la fonction de répartition de la loi normale centrée réduite, la proba précédente est égale à

Il reste à résoudre

PS : c'est tres gentil de ta part de nous faire partager ta connaissance.

[Guga78]

ho un itinien lol

[nuage]

Oui, on utilise la table de la loi normale :

pour ne pas trop me fatiguer je pose .
On a


On cherche alors dans la table les valeurs de telles que :
on lit et donc la plus petite valeur possible pour t est entre 2,05 et 2,06.
En prenant t=2,06 on résout .
Ce qui me permet de constater que la valeur que j'ai donnée précédemment est fausse. Le calcul mental ne me réussit pas. La valeur minimum est entre 950 et 954. Là je l'ai fait à la machine :zen:.


Ps:

ho un itinien lol

C'est quoi un itinien ?

[modification]
je ne suis pas d'accord avec all : l'univers est l'ensemble des n observations. Qu'après ça on ne retienne qu'une partie des données est un autre problème.
Pour le passage à la fonction de répartition :
par définition.
On en déduit
(extrémité moins origine)
Et, compte tenue de la symétrie des lois normales

[all]

Merci, j'ai compris maintenant ^_^.

Pour l'univers je t'avoue que je ne sais pas trop quoi penser :/

Un itinien c'est un étudiant de l'itin

[all]

Bonsoir j'ai fait les 2 premiere question de l'exercice 3 en suivant mon cours mais 1/ je ne suis pas sur de ce que j'ai fait 2/je n'ai pas tout compris à ce que j'ai fait.

Je me permet de poster ma copie ^_^



cordialement,

all

[Guga78]

Bonsoir Nuage,

Merci pour cette précision c'est effectivement plus clair.
En fait ce devoir est un devoir de rattrapage pour les etudiants de l'itin qui est une ecole d'informatique.
Voila :we:
Je te remercie encore du temps que tu nous consacre!! Car c'est franchement pas simple pour des "non-matheux".

[cmoi74]

Salut,

j'ai moi aussi ces exercices a faire et je n'arrive pas à comprendre comment tu passes de


à ca :



Si tu voulais bien m'expliquer ca, ce serait génial :p