[résolu][mpsi] récurrence de Un
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 12:34
par NazDreG » 16 Sep 2007, 12:34
Soit Un avec n appartient à N étoile la suite définie par :
U1 = 1 et Un+1 = 1 + (n/Un)
Montrer que pour tout n de N étoile :
(1+RACINE(4n-3))/2 =< Un =< (1+RACINE(4n+1))/2
Je pense qu'il faut faire une récurrence, j'ai démontré l'initialisation mais après pour montrer Pn => Pn+1 j'y arrive pas trop :marteau:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 12:47
par fahr451 » 16 Sep 2007, 12:47
que dire de la fonction f(x) = 1+ n/x ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Sep 2007, 12:48
par yos » 16 Sep 2007, 12:48
Bonjour.
Expression conjuguée.
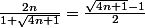
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 13:02
par NazDreG » 16 Sep 2007, 13:02
en effet ça marche bien pour cette expression mais pour l'autre quand je développe je trouve :
2n/(1+Racine(4n-3)) = [n - n*Racine(4n-3)] / (2 - 2n)
Erreur de calcul? mauvaise méthode?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Sep 2007, 13:05
par yos » 16 Sep 2007, 13:05
NazDreG a écrit:Erreur de calcul? mauvaise méthode?
Non c'est bon. Il te reste à le comparer à ce que tu veux.
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 13:41
par NazDreG » 16 Sep 2007, 13:41
quelqu'un a une idée pour montrer que
}{(2-2n)} \ge \frac{(1+\sqrt{4n+1})}{2})
?
il me manque plus que ça pour ma récurrence
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 16:06
par NazDreG » 16 Sep 2007, 16:06
petit up, personne ne trouve? :hum:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 16:34
par fahr451 » 16 Sep 2007, 16:34
sisi j'ai trouvé il m ' a fallu deux minutes...
inutile d'écrire "personne ne trouve" c'est désobligeant
on doit montrer que
4n >= (1+rac (4n+1) ) ( 1 +rac (4n-3) )
montre que
rac(4n-3) +1 >= rac(4n+1) -1
en élevant au carré froidement
et ensuite c'est fini
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 16:56
par NazDreG » 16 Sep 2007, 16:56
salut,
désolé si je t'ai paru désobligeant je voulais juste essayer de réanimer le sujet.
concernant ta réponse je ne la comprend pas trop est-ce que tu pourrais l'expliciter s'il-te-plait?
(tu commence par montrons que 4n >=... c'est une transformation de mon inégalité? comment as-tu fait? ensuite tu me propose de montrer une autre inégalité mais je n'arrive pas à faire le lien.. voilà désolé j'ai un peu de mal même en réflechissant sur papier)
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 18:13
par NazDreG » 16 Sep 2007, 18:13
Toujours pas trouvé :cry:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Sep 2007, 20:07
par yos » 16 Sep 2007, 20:07
J'obtiens comme majorant de

le nombre

et il faut que tu prouves que ce nombre est plus petit que

. Cela revient à prouver que
\sqrt{4n+5})
. On élève au carré et on tombe sur une inégalité facile :

.
Je n'ai pas vérifié mes calculs : il te reste ce travail.
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 21:10
par NazDreG » 16 Sep 2007, 21:10
il y a un (n-2) qui s'est perdu en route?
de plus ton inégalité "facile" n'est pas vérifiée pour les premières valeurs de n..
-
NazDreG
- Membre Naturel
- Messages: 40
- Enregistré le: 19 Juin 2007, 12:23
-
 par NazDreG » 16 Sep 2007, 21:42
par NazDreG » 16 Sep 2007, 21:42
c'est bon j'ai réussi à m'en sortir je retombe sur une inégalité avec un trinome et 0, merci à tous pour votre aide :++:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Sep 2007, 21:53
par yos » 16 Sep 2007, 21:53
Coquilles corrigées.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
