bon vuala jai un ptit probleme avec une etude de fonction , enfin surtout avec le signe de sa dérivée
on a f(x)= [(x+y)/2]^p - [(x^p + y^p)/2] avec p fixé N et y fixé positif.et Df=R
on trouve (sauf erreur de ma part) f'(x)= (p/2) [[(x+y)/2]^(p-1) - (x^(p-1))]
Le probleme est que je ne vois pas comment factoriser [[(x+y)/2]^(p-1) - (x^(p-1))] afin d'étudier le signe :cry:
toute aide serai la bienvenue lol et merci d'avance
Probleme avec une fonction
9 messages
- Page 1 sur 1
reponse
salut
pour factoriser tu dois utiliser la formule suivante :
a^n - b^n = (a-b) . S
où S = somme de k=0 à n-1 de (a^k).(b^(n-1-k))
ici a=(x+y)/2 , b=x et n=p-1
Voila
et il reste f '(x)= ((y-x)/2) fois une somme à travailler
Bon courage !!
pour factoriser tu dois utiliser la formule suivante :
a^n - b^n = (a-b) . S
où S = somme de k=0 à n-1 de (a^k).(b^(n-1-k))
ici a=(x+y)/2 , b=x et n=p-1
Voila
et il reste f '(x)= ((y-x)/2) fois une somme à travailler
Bon courage !!
merci !
c'est justement ce que j'avais fait mais en fait jai mal formulé ma question
parce qu'n fait, en factorisant de cette façon, je n'arrive pas a avoir le signe de la somme : en effet, si x<0, alors sa va dependre du fait ke p soit pair ou non, de la valeur de k , etc.... de plus, comme c'est une somme, sa me semble impossible
Soit je m'y prend mal soit y faut kje trouve une autre factorisation
si vs pouvez m'aider ...
c'est justement ce que j'avais fait mais en fait jai mal formulé ma question
parce qu'n fait, en factorisant de cette façon, je n'arrive pas a avoir le signe de la somme : en effet, si x<0, alors sa va dependre du fait ke p soit pair ou non, de la valeur de k , etc.... de plus, comme c'est une somme, sa me semble impossible
Soit je m'y prend mal soit y faut kje trouve une autre factorisation
si vs pouvez m'aider ...
Bonjour,
Si tu veux de l'aide :
1. utilise LaTeX, car tes messages sont très difficiles à lire, et ne donnent pas envie de s'y plonger
2. écris en français
3. indique ce que tu as déjà fait : cela évitera à ceux qui veulent t'aider de tout refaire.
La suggestion de stéphanie13 permet tout de même d'avancer un peu, non ?
=(\frac{x+y}{2})^p-\frac{x^p+y^p}{2})
=\frac{p}{2}[(\frac{x+y}{2})^{p-1}-x^{p-1}])
On utilise :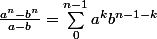
=\frac{p}{2}\frac{x-y}{2}\sum_0^{p-2}\frac{1}{2^k}(x+y)^{k}x^{p-2-k})
Deux premières conclusions :
si alors tous les termes de la somme sont positifs et
alors tous les termes de la somme sont positifs et ) est du signe de
est du signe de 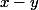
si alors tous les termes de la somme sont positifs et
alors tous les termes de la somme sont positifs et ) est du signe de
est du signe de 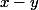
Sauf erreur.
Nicolas
Si tu veux de l'aide :
1. utilise LaTeX, car tes messages sont très difficiles à lire, et ne donnent pas envie de s'y plonger
2. écris en français
3. indique ce que tu as déjà fait : cela évitera à ceux qui veulent t'aider de tout refaire.
La suggestion de stéphanie13 permet tout de même d'avancer un peu, non ?
On utilise :
Deux premières conclusions :
si
si
Sauf erreur.
Nicolas
merci nicolas !
Desolé de ne pas utiliser Latex , mais je ne savais même pas que ça existait.
Ton expliquation est juste, c'est exactement les conclusions auxquelles je suis arrivé
Cependant, si x<-y, p entre en jeu : je veux dire en fait que selon si p est pair ou p est impair, il faudrai distinguer 2 cas
J'en suis arrivé (sauf erreur de ma part) a cette conclusion :
- si p est pair, alors tous les termes de la somme sont positifs
- si p est impair , alors tous les termes de la somme sont négatifs
Encore une petite interrogation : comment connaitre le signe de la somme pour -y
PS: si quelqu'un pouvait me dire comment utiliser et trouver Latex, ça serait sympa :we:
Desolé de ne pas utiliser Latex , mais je ne savais même pas que ça existait.
Ton expliquation est juste, c'est exactement les conclusions auxquelles je suis arrivé
Cependant, si x<-y, p entre en jeu : je veux dire en fait que selon si p est pair ou p est impair, il faudrai distinguer 2 cas
J'en suis arrivé (sauf erreur de ma part) a cette conclusion :
- si p est pair, alors tous les termes de la somme sont positifs
- si p est impair , alors tous les termes de la somme sont négatifs
Encore une petite interrogation : comment connaitre le signe de la somme pour -y
PS: si quelqu'un pouvait me dire comment utiliser et trouver Latex, ça serait sympa :we:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
