Tribus

par **legeniedesalpages** » 05 Sep 2007, 11:51

Bonjour,

j'ai un problème avec cet exercice:

Soit

une partition de

.
Montrer que

avec

et

.

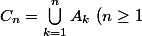En notant

, je me demandais si

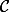
est une tribu.

Par exemple si je prends un élément

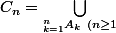son complémentaire sera

qui n'est pas dans

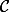
, non?

Edit: Si

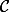
n'est pas une tribu, alors je ne vois pas comment je peux montrer cette égalité.

D'ailleurs si l'un des

est non vide et

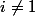
, alors

, mais

. Comme on essaie de montrer cette égalité pour une quelconque partition d'un quelconque ensemble

, l'égalité est fausse non?

Merci pour vos indications.

par **Pouick** » 05 Sep 2007, 13:08

hmmm ..moui c curieux cette histoire ^^

par **legeniedesalpages** » 05 Sep 2007, 13:19

Bonjour Pouick, à mon avis il y a un bug dans l'énoncé. Peut-être en modifiant l'ensemble d'indices on pourrait arriver à quelque chose de cohérent. Je susi en train de chercher.

par **Pouick** » 05 Sep 2007, 14:12

Mais j'ai deja fait un exo dans ce style... faut que je m'en souvienne a present ^^

par **Pouick** » 05 Sep 2007, 14:14

Pour moi ca serait plutot a prouver une egalité entre 2 tribu... Mais de toute maniere puisque les (Ai) forment une partition de E , la tribu engendré n'est pas bien grande .. on y ajoute seulement toutes les reunions possible des Ai ...

si on essai de tourner l'exo autour des Cn comme ils sont proposé... peut etre s'agirait il de montrer que la tribu engendrer par les Cn est la meme que la tribu engendrer par les An ...

par **legeniedesalpages** » 05 Sep 2007, 14:16

ou t es plus jeune que ce que je pensais, ou t as une sacré bonne mémoire lol

:lol: :lol: :lol:

par **Pouick** » 05 Sep 2007, 14:17

lol ... ha bon tu pensais que j'avais quel age ? 34 ans ? :ptdr:

par **legeniedesalpages** » 05 Sep 2007, 14:29

Pouick a écrit: si on essai de tourner l'exo autour des Cn comme ils sont proposé... peut etre s'agirait il de montrer que la tribu engendrer par les Cn est la meme que la tribu engendrer par les An ...

ça parait presque évident pourtant. on a

, vu qu'une tribu est stable par union dénombrable.

Donc

et

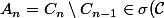pour tout

.

Donc

, et donc

, non?

par **legeniedesalpages** » 05 Sep 2007, 14:30

Pouick a écrit:lol ... ha bon tu pensais que j'avais quel age ? 34 ans ? :ptdr:

quand meme pas, je te voyais plutôt en master ou en doctorat, et cet exo c'est plutôt niveau prepa/licence non?

ça doit surment remonter à loin.

par **Pouick** » 05 Sep 2007, 14:31

lol ...bin oué ^^ c pas specialement dur a prouver ... ca c sur ... Mais bon au moins c pas faux comme question :ptdr:

par **Pouick** » 05 Sep 2007, 14:33

Bin je suis en Master 2 cette année.. donc ca remonte a 2 ans maintenant... puis comme j'ai pas fait prepa .. c pas la bas que je l'ai fait... c fou ca .. tu as attaqué les tribus en Prepa? .. tu me diras.. y a pas d'age ... :we:

par **legeniedesalpages** » 05 Sep 2007, 14:43

lol non moi non plus j'ai jamais fait prépa. On avait attaqué les tribus en deuxieme année de fac, en probas.

Enfin là j'ai trouvé un exo sur google qui a l'air de coller (http://www.iecn.u-nancy.fr/~chassain/S6/exostribus-version2.pdf exercice 7_a)

Je pense qu'on peut donc modifier l'ensemble :

et

Je vérifie si ça marche.

par **Pouick** » 05 Sep 2007, 15:02

ha bin vi ca marche aussî ^^

par **Pouick** » 05 Sep 2007, 15:03

en gros c juste histoire de dire que y a toutes les reunions possible de An

par **legeniedesalpages** » 05 Sep 2007, 15:07

ok, je vais bosser puis je reviens m y pencher dessus. à plus

Tribus

tribus

Qui est en ligne