Série astucieuse
Olympiades mathématiques, énigmes et défis
-
bdupont
- Membre Relatif
- Messages: 132
- Enregistré le: 16 Juin 2005, 15:11
-
 par bdupont » 04 Sep 2007, 20:05
par bdupont » 04 Sep 2007, 20:05
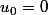
et
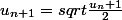
On demande de trouver le produit P de la série
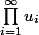
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Sep 2007, 20:12
par Nightmare » 04 Sep 2007, 20:12
Salut :happy3:
J'ai réussi à prouver déjà que le terme général de un est cos(pi/(2^(n+1)))
Je cherche la convergence du produit maintenant.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Sep 2007, 21:27
par Joker62 » 04 Sep 2007, 21:27
u_1 = V2/2
et cos(pi/2) = 0
T'as dû te planter na Nightmare ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Sep 2007, 21:30
par Nightmare » 04 Sep 2007, 21:30
u1=cos(pi/4) :lol3:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Sep 2007, 21:33
par Joker62 » 04 Sep 2007, 21:33
Ah vui :id:
J'ai pas fait tilt :D
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Sep 2007, 21:35
par Nightmare » 04 Sep 2007, 21:35
Joker62 a écrit:J'ai pas fait tilt

Pourtant tu m'as fait flipper...
(Désolé, je sors!)
-
bdupont
- Membre Relatif
- Messages: 132
- Enregistré le: 16 Juin 2005, 15:11
-
 par bdupont » 04 Sep 2007, 21:40
par bdupont » 04 Sep 2007, 21:40
Besoin d'un tuyau?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Sep 2007, 21:40
par Joker62 » 04 Sep 2007, 21:40
Mouahahahhaha, tant que tu perds pas tes boules...
Ok j'te suit :D
-
bdupont
- Membre Relatif
- Messages: 132
- Enregistré le: 16 Juin 2005, 15:11
-
 par bdupont » 04 Sep 2007, 21:45
par bdupont » 04 Sep 2007, 21:45
Penser à la fonction sin(x)/x
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 04 Sep 2007, 22:44
par fahr451 » 04 Sep 2007, 22:44
multiplier le produit de rang n par sin (pi/2^(n+1) ) et "penser à"
sin x cos x = sin (2x) /2
on a inventé le mouvement (presque) perpétuel
un grand classique de lycée non?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Sep 2007, 22:56
par Joker62 » 04 Sep 2007, 22:56
Lol :)
Purée ouai, vu comme ça :D
-
Bouchra
- Membre Relatif
- Messages: 113
- Enregistré le: 13 Juil 2006, 15:38
-
 par Bouchra » 06 Sep 2007, 13:28
par Bouchra » 06 Sep 2007, 13:28
Dans le même esprit,
calculer pour tout réel a différent de

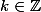
:

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
