Levée d'indétermination

par **MathsAngel** » 02 Sep 2007, 12:49

Bonjour,

je dois calculer la limite en l'infini de: 2x² - racine de x
Je bloque totalement... Comment lever cette indétemination ? AUriez-vous une méthode ? :help: Merci d'avance

par **fonfon** » 02 Sep 2007, 12:51

salut,

par **MathsAngel** » 02 Sep 2007, 12:55

A ok, grace aux quantités conjuguées... Merci, je vais essayer ça :we:

par **fonfon** » 02 Sep 2007, 13:00

A ok, grace aux quantités conjuguées...

oui, sans oublier apres que en +inf ou -inf la limite d'une fonction rationnelle est la même que le quotient de ses termes de + haut degré

par **oscar** » 02 Sep 2007, 13:00

Bonjour

Multiplier le binôme conjugué
Au départ si x--> -oo ,Vx n' a pas de sens; sinon on a oo-oo indéterminé.

A=(2x²- vx)(2x²+vx)/(2x²+vx)=( 4x^4-x)/(2x²+vx)
lim A si x--> +oo,A---> +oo etsi x--> -oo; pas de sxens
(la différence de degrés entre numérateur et d'nominateur = 2)

par **MathsAngel** » 02 Sep 2007, 13:02

Et puis, la limite en 0 de : sin(x+pi)/x

Il faut que j'utilise un encadrement ( pour arriver au théorème des gendarmes) ?
Si oui, alors j'aurais pour commencer:
-pi < sin(x+pi) < pi

??? :hum:

par **fonfon** » 02 Sep 2007, 13:05

re,

rappel: sin(x+pi)=-sin(x)

par **MathsAngel** » 02 Sep 2007, 13:09

Pfff oui, je n'ai pas assez réfléchi là. :doh:
Merci :we:

par **Nightmare** » 02 Sep 2007, 13:11

Pourquoi la quantité conjuguée dans le premier ?

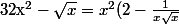qui diverge clairement vers +oo.

par **fonfon** » 02 Sep 2007, 13:13

Nightmare a écrit:Pourquoi la quantité conjuguée dans le premier ?

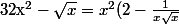qui diverge clairement vers +oo.

d'accord avec toi mais je pense que beaucoup ne le verrait pas

par **MathsAngel** » 02 Sep 2007, 14:28

Oui, faut avoir une bonne intuition mathématique pour y arriver :we:

par **fonfon** » 02 Sep 2007, 14:36

pour Nightmare c'est normal, mais si toi tu ne le vois pas de suite applique ce qui te semble le plus facile plutôt que de perdre du temps le jour d'un DS

Levée d'indétermination

Levée d'indétermination

Qui est en ligne