Sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maxboubou
- Membre Relatif
- Messages: 109
- Enregistré le: 16 Déc 2006, 19:22
-
 par maxboubou » 01 Sep 2007, 16:14
par maxboubou » 01 Sep 2007, 16:14
Bonjour, comment calculer les deux sommes suivantes :
somme (k^2*(k parmi n)) avec k variant de 0 a n
(0 parmi n) + (2 parmi n) + (4 parmi n)..................
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 01 Sep 2007, 16:18
par Joker62 » 01 Sep 2007, 16:18

on est d'accord ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Sep 2007, 16:24
par Nightmare » 01 Sep 2007, 16:24
Bonjour, pour la deuxième, considère la somme avec les nombres impairs :
(1 parmi n) + ...+ (E(n/2) parmi n). Somme les deux somme et utilise le binôme de newton
-
maxboubou
- Membre Relatif
- Messages: 109
- Enregistré le: 16 Déc 2006, 19:22
-
 par maxboubou » 01 Sep 2007, 16:25
par maxboubou » 01 Sep 2007, 16:25
Pour joker :
oui,c ca (c'est quoi le code pour marquer les sommes ?)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Sep 2007, 16:42
par aviateurpilot » 01 Sep 2007, 16:42
^n=\bigsum_{k\ pair\in\{1,2,..,n\}}+\bigsum_{k\ impair\in\{1,2,..,n\}}=2^n)
^n=\bigsum_{k\ pair\in\{1,2,..,n\}}-\bigsum_{k\ impair\in\{1,2,..,n\}}=0)
d'ou


donne
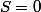

donne

pour
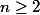
pour

pose
=(x+1)^n)
on a donc
=f"(1)=\bigsum_{k=0}^{n}k^2C_{n}^{k}-\bigsum_{k=0}^{n}kC_{n}^{k})
et on a
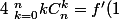=n2^{n-1})
d'ou
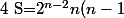+n2^{n-1}=2^{n-2}n(n+1))
mtn on remarque que
})
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Sep 2007, 16:45
par Flodelarab » 01 Sep 2007, 16:45
maxboubou a écrit:Pour joker :
oui,c ca (c'est quoi le code pour marquer les sommes ?)
C'est du latex.
Regarde
ICI
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 01 Sep 2007, 16:52
par Edrukel » 01 Sep 2007, 16:52
-
maxboubou
- Membre Relatif
- Messages: 109
- Enregistré le: 16 Déc 2006, 19:22
-
 par maxboubou » 01 Sep 2007, 17:20
par maxboubou » 01 Sep 2007, 17:20
merci a tous ! (l'aviateur, c'est pas plutot 2^(n-2) a la fin de ta preuve ?)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Sep 2007, 20:35
par aviateurpilot » 01 Sep 2007, 20:35
maxboubou a écrit:merci a tous ! (l'aviateur, c'est pas plutot 2^(n-2) a la fin de ta preuve ?)
oui, j'ai modifier
-
Bouchra
- Membre Relatif
- Messages: 113
- Enregistré le: 13 Juil 2006, 15:38
-
 par Bouchra » 01 Sep 2007, 21:32
par Bouchra » 01 Sep 2007, 21:32
En tout cas la généralisation du site est incroyable, je connaissais.
Avant de l'avoir vue, j'avais fait:
= \Bigsum_{k=1}^{n} k^m C_n ^k x^k)
Avec des cas particuliers on voit facilement que :
=\Bigsum_{i=1}^{m} a_{im} \frac{n!}{(n-i)!} x^i (1+x)^{n-i})
avec :
 = x(I_m)'(x))
qui donne une relation intéressante entre les

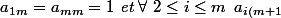} = i \cdot a_{im} + a_{(i-1)m})
De là faut déduire la formule de a_im.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités

 on est d'accord ?
on est d'accord ?