Bonjour
Pourriez-vous m'aider à résoudre cette équation:
|z+1| = |1/z| avec z C
J'ai déjà trouvé quatres solutions mais je doute que ma méthode soit rigoureuse.
On suppose z R, l'équation se ramène à du second degré réel. On trouve z = (V5-1)/2 ou z = -(V5+1)/2
On suppose z U soit z = e^ix et l'on trouve z = e^(2i*pi/3) ou z = e^(-2i*pi/3)
Merci d'avance de votre aide.
Module z+1 = module 1/z
10 messages
- Page 1 sur 1
Peut-être que quelque chose m'échappe, mais je ne vois pas de solution analytique simple. L'équation peut se réécrire :
|=1) (dont
(dont 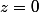 n'est pas solution).
n'est pas solution).
Cela équivaut à l'existence de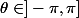 tel qu'on ait :
tel qu'on ait :
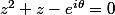 .
.
Cette équation du second degré a pour discriminant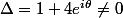 et a donc deux solutions.
et a donc deux solutions.
Plus précisément, pour toute valeur de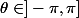 , les solutions correspondantes sont
, les solutions correspondantes sont ) et
et ) , où
, où  désigne l'une des racines carrées de
désigne l'une des racines carrées de 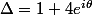 .
.
Cela équivaut à l'existence de
Cette équation du second degré a pour discriminant
Plus précisément, pour toute valeur de
P.-S. : On sait que tout nombre complexe non nul  possède deux racines carrées opposées
possède deux racines carrées opposées  et
et  , qu'on peut expliciter, mais l'expression obtenue ici ne sera pas jolie jolie, sauf pour des valeurs particulières de
, qu'on peut expliciter, mais l'expression obtenue ici ne sera pas jolie jolie, sauf pour des valeurs particulières de  comme
comme 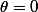 ou
ou 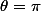 , qui doivent redonner tes solutions réelles ou de module un (je n'ai pas vérifié tes calculs).
, qui doivent redonner tes solutions réelles ou de module un (je n'ai pas vérifié tes calculs).
Un complexe  est de module un si et seulement s'il existe
est de module un si et seulement s'il existe 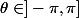 tel que
tel que 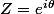 . On applique cela dans notre situation à
. On applique cela dans notre situation à 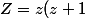) .
.
P.-S. : N'hésite pas à me dire "tu" plutôt que "vous" ; sur internet, je trouve ça plus convivial, et puis ici, nous sommes tous égaux. :++:
Edit : Mon message fait doublon avec celui de Galt, une fois de plus mon petit cerveau a été trop lent ! :--:
P.-S. : N'hésite pas à me dire "tu" plutôt que "vous" ; sur internet, je trouve ça plus convivial, et puis ici, nous sommes tous égaux. :++:
Edit : Mon message fait doublon avec celui de Galt, une fois de plus mon petit cerveau a été trop lent ! :--:
Un moment de désuvrement ? Une envie furieuse de taper une formule compliquée avec 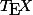 ? Je ne sais pas pourquoi je l'ai fait, mais j'ai explicité les solutions. Tous calculs faits, on trouve que l'ensemble des solutions de l'équation
? Je ne sais pas pourquoi je l'ai fait, mais j'ai explicité les solutions. Tous calculs faits, on trouve que l'ensemble des solutions de l'équation 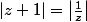 est :
est :
\right]|(t,\sigma_1,\sigma_2)\in[-1,+1]\times\{-1,+1\}\times\{-1,+1\}\right}) .
.
Pour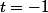 et
et 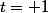 , on retrouve les solutions particulières données par evilangelium. On a d'autres solutions dont l'expression algébrique est assez simple, obtenues pour
, on retrouve les solutions particulières données par evilangelium. On a d'autres solutions dont l'expression algébrique est assez simple, obtenues pour 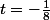 :
: 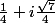 ,
, 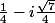 ,
, 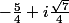 et
et 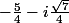 . Mais pour les autres valeurs de
. Mais pour les autres valeurs de  , ça n'a pas l'air très appétissant. :doh:
, ça n'a pas l'air très appétissant. :doh:
Pour
Je suis en effet nul en calcul, c'est un miracle si ce que j'ai fait est juste :lol2: ; et pourtant, ça en a l'air !
Je suis prof dans un lycée des Hauts-de-Seine pas spécialement connu ni prestigieux (mais néanmoins agréable) ; je n'en dis pas plus en public, comme ça je pourrai continuer à écrire des bêtises ici sans être reconnu. :lol3:
Je suis prof dans un lycée des Hauts-de-Seine pas spécialement connu ni prestigieux (mais néanmoins agréable) ; je n'en dis pas plus en public, comme ça je pourrai continuer à écrire des bêtises ici sans être reconnu. :lol3:
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
