Démonstration : intégrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 19:51
par lapras » 30 Aoû 2007, 19:51
Il ne me reste donc plus qu'a démontrer la "technique de changement de variable" que tu as utilisé, si j'ai bien compris :
INT[a...b](f(x) dx) = INT[a'...b'](f°g(x').g'(x')dx')
si g(a') = a et g(b') = b
avec g une application et g(x') = x
Reste à le prouver :
INT[a...b](f(x) dx) = F(b) - F(a)
INT[a'...b'](f°g(x').g'(x')dx') = INT[a'...b'](F'°g(x').g'(x')dx')
Dérivée de fonction composée...
INT[a'...b'](f°g(x').g'(x')dx') = F(g(a')) - F(g(b')) = F(a) - F(b)
cqfd ????
:ptdr:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 30 Aoû 2007, 20:03
par Skullkid » 30 Aoû 2007, 20:03
Pour faire la "vraie" démonstration, faut tenir compte de certaines hypothèses (comme le fait que g doit être
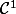
sur [a',b'], c'est-à-dire dérivable et à dérivée continue, et que
\subset I)
avec I un intervalle où f est continue). Mais sinon c'est bien ça la démo ^^
PS : tu peux utiliser les balises [tex], ça rendrait tes calculs plus lisibles...(plus longs à écrire aussi, certes)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 20:04
par lapras » 30 Aoû 2007, 20:04
Ok merci skullkid :id:
Bon bah je me sens soulagé je vais pouvoir enfin démontrer une formule que j'ai admise depuis la 6eme : PI R²
:++:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 22:42
par Nightmare » 30 Aoû 2007, 22:42
En fait comme je l'ai dit, une intégrale c'est une somme, une sorte de somme de rectangle (C'est la construction de l'intégrale de Riemann), mais une somme continue, et les bases des rectangles se construise suivant un déplacement qui est représenté par ce dx.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 22:45
par Nightmare » 30 Aoû 2007, 22:45
En tout cas c'est bien de voir que le calcul d'intégrale t'interresse. Mais ce qui est encore plus interressant c'est son application.
Par exemple, essaye de montrer avec des intégrale que la série harmonique diverge (c'est à dire que la suite définie par

n'admet pas de limite).
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 30 Aoû 2007, 22:48
par Sylar » 30 Aoû 2007, 22:48
Salut :
diverger = n'a pas de limite ??
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 22:53
par Nightmare » 30 Aoû 2007, 22:53
Oui j'allais me corriger : Ou tend vers oo.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 22:53
par lapras » 30 Aoû 2007, 22:53
diverger = Pas de limite finie (elle ne converge pas)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 23:06
par Nightmare » 30 Aoû 2007, 23:06
Donc, une idée Lapras?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 23:07
par lapras » 30 Aoû 2007, 23:07
Oué, deux secondes je la poste des que je suis sur.
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 30 Aoû 2007, 23:23
par Sylar » 30 Aoû 2007, 23:23
lapras a écrit:diverger = Pas de limite finie (elle ne converge pas)
Diverger= limite égale a l'infini ou pas de limite
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 30 Aoû 2007, 23:26
par Sylar » 30 Aoû 2007, 23:26
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 23:27
par lapras » 30 Aoû 2007, 23:27
donc :
Calcul de :
int[0...1]( 1/x dx) = [ln(x)] = ln(1) - ln(0)
or.......................................k=n....................k=n
int[0...1]( 1/x dx) = lim (1/n) * Epsilon(n/k) = lim Epsilon(1/k)
...........................n->+OO......k=1........n->+OO k=1
or ln(1) - ln(0) tend vers +OO quand x->0
donc
lim Epsilon(1/k) = +OO
x->+OO
CQFD ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 23:27
par Nightmare » 30 Aoû 2007, 23:27
Utile ce lien, tu ne vois pas que j'essaye de le faire chercher sylar?
Qui plus est, "diverger = ne pas avoir de limite finie" est une définition correcte, je ne vois pas pourquoi tu reprends Lapras.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 23:28
par lapras » 30 Aoû 2007, 23:28
:++: Moi j'ai chercher
Mais ca se trouve j'ai faux, si oui, dis moi juste que c'est faux, je chercherai une autre soluce
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 23:28
par Nightmare » 30 Aoû 2007, 23:28
Je ne comprends pas ce passage :
"lim (1/n) * Epsilon(n/k) = lim Epsilon(1/k)"
Au passage, le signe de somme, c'est un grand sigma et non un epsilon :lol2:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 23:31
par lapras » 30 Aoû 2007, 23:31
Lol moi et le grec...
je voulais dire que :
...........k=n............................................................k=n
(1/n) * Sigma(n/k) = (1/n) * n(1/1 + 1/2 + ... + 1/n) = sigma(1/k)
..........k=1.............................................................k=1
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Aoû 2007, 23:36
par Nightmare » 30 Aoû 2007, 23:36
Non tu ne peux pas diviser par n comme ça, vu que dans la somme il est variable !
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Aoû 2007, 23:38
par lapras » 30 Aoû 2007, 23:38
mais c'est k qui est variable, pas n
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 30 Aoû 2007, 23:45
par Sylar » 30 Aoû 2007, 23:45
Nightmare a écrit:Utile ce lien, tu ne vois pas que j'essaye de le faire chercher sylar?
Qui plus est, "diverger = ne pas avoir de limite finie" est une définition correcte, je ne vois pas pourquoi tu reprends Lapras.
C'est parce qu'il y a plusieurs méthodes de résolution ........
Et diverger vers +infini c'est pas pareil que ne pas avoir de limite .....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
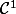 sur [a',b'], c'est-à-dire dérivable et à dérivée continue, et que
sur [a',b'], c'est-à-dire dérivable et à dérivée continue, et que \subset I) avec I un intervalle où f est continue). Mais sinon c'est bien ça la démo ^^
avec I un intervalle où f est continue). Mais sinon c'est bien ça la démo ^^