Topologie: homéomorphismes

[Yipee]

Je crois pas : essaie avec deux éléments Y, Y' dénombrables (infinis) et Z, Z'.
Tu as une application croissante et une autre . Comment définis-tu l'application de dans pour que la croissance soit préservée?

Le truc est que ma partie est supposée totalement ordonnée. De ce fait, s'il n'y a que deux éléments, on a et (on dans l'autre sens). Par définition de la relation d'ordre, f est une restriction de g.

[yos]

OK avec une partie totalement ordonnée (ça revient à mes ), mais tu l'avais pas mis dans ton premier message et j'ai lu trop vite le suivant.

[Yipee]

En fait en y réfléchissant un peu, je ne suis pas sur que le fait d'avoir un élément maximal permette de conclure (à ma décharge, il n'est pas simple de se concentrer en tondant sa pelouse :ptdr: )

[yos]

avec , on est sûr que A est l'élément maximal cherché.

[Yipee]

A creuser mais prouver l'inductivité avec Y,Y' et Z,Z' dénombrables me semble aussi dur que la question de départ.

On peut peut-être faire ceci avec ton idée :

soit une bijection de sur A et une bijection de sur B.

Pour n fixé, on prend et une bijection croissante de sur .
Il est clair qu'on peut construire les par récurrence de façon que la restriction de à soit .
Bref je travaille avec un ensemble plus petit qui, lui, est clairement inductif.

Je ne pense pas que cette construction marche aussi simplement. La restriction de à ne sera pas obligatoirement . En fait je pense qu'il ne faut pas prendre initialement la bijection de sur B. On la construit aussi par récurrence.

[yos]

c'est la suite qu'on construit par récurrence de façon que restreint à soit précisément .

[yos]

Ah oui il y a un problème! Je n'ai pas l'excuse du gazon. Moi c'est "Lost" qui m'a perdu. Je pense qu'on peut s'en sortir tout de même.

[Yipee]

Oui, la solution est de construire la bijection dans la récurrence. Précisément, soit i compris entre 1 et n tel que il faut prendre compris entre et . Mais je ne suis pas sur que cela fonctionne réellement. Il faudrait essayer de l'écrire sérieusement (sans pelouse ni Lost...).

[yos]

Je pense plutôt qu'on se donne et , et qu'on construit et par récurrence mais de façon un peu plus subtile :
,
si sont rangés dans le même ordre que , on pose , sinon, on introduit en plus dans des bien choisis entre les autres (et pareil pour ). On peut ainsi s'arranger pour que restreint à soit .

J'ai confiance dans cette méthode car elle utilise de façon essentielle la densité de A et de B dans ]0,1[. Je n'ai pas le temps de regarder les détails ni de rédiger.

[yos]

Reprenons!
une bijection de N sur A, une bijection de N sur B.
On construit par récurrence de la façon suivante :

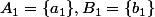
1. , évidente.
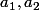
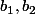
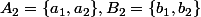
2. Si sont rangés dans le même ordre que , on pose et est évidente, sinon, on a par exemple , auquel cas on considère dans A tel que et on envoie sur respectivement. On a la croissance et le fait que la restriction à est .
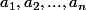
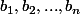
3. Supposons construit comme il faut : contient au moins , contient au moins , et est une bijection croissante de sur .
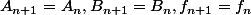
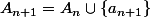
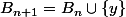
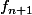
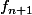
On note les éléments de dans l'ordre croissant et les éléments de dans l'ordre croissant.Si et , on pose . Sinon, on a par exemple , auquel cas on pose et , y étant un élément de B compris entre et prolonge alors de façon évidente en posant , et est croissante par construction.

On conclut par inductivité.

[namfoodle sheppen]

on ne peut pas juste dire qu'il existe une application croissante de A dans N et de B dans N ? je ne vois pas pourquoi ...

[yos]

Dans A les éléments n'ont pas de successeur par exemple.

[Yipee]

La construction de yos semble presque marcher. Mais je ne pense pas que l'on puisse assurer ainsi que . Il doit falloir considérer le cas où et l'ajouter à la main comme pour .

En tout cas bravo pour l'avoir rédigé.

[yos]

Oui je l'ai pas écrit mais il faut faire pareil si : on lui ajoute un antécédent dans .
Et bravo pour avoir eu le courage de me lire.