Démonstration : intégrales

[lapras]

Bonjour à tous,
j'aimerais démontrer ce théoreme :
"si f est une fonction continue sur un intervalle I, et si a appartient à I, la
x
fonction F(x) = Intégrale(f(t) dt)
a

est l'unnique primitive de f s'annulant en a"

Je sais bien qu'en faisant un cas par cas (par ex. avec la fonction carré), on remarque ceci, mais comment le démontrer pour un cas général ?
Malheureusement ce théoreme est ADMIS en classe de terminale...:--:
Or je ne peux pas regarder un théoreme si je ne peux pas le démontrer, s'il vous plait aidez moi.
Lapras

[Sylar]

Tu veux déja t'attaquer au programme de sup ?!

[lapras]

Oui je préfere, car pour moi admettre un théoreme c'est un crime. (hyperbole)

[Alpha]

Oui je préfere, car pour moi admettre un théoreme c'est un crime. (hyperbole)

Alors beaucoup de physiciens sont des criminels :zen:

[lapras]

C'est pour ça que au lieu de faire de la physique cet été j'ai fait des maths (car admettre des théoremes basés sur l'expérimentation c'est un peu dur, même si c'est interessant !)

[Sylar]

Notons:


F(x)=Int[ a ... x] f(t) dt

F(b)= Int[a..b] f(t)dt

Soit G une primitive de f alors il existe k réel tel que :

F(x)=G(x)+k

Or :F(a)=0 => G(a)=-k

=> F(x)=G(x) - G(a)

=> F(b)=G(b)-G(a)

Int[a..b] f(t)dt =F(b)= G(b) -G(a)

[lapras]

Sylar, ca je l'ai déja démontré,
mais ce que je veux démontrer c'est que :
F(x)=Int[ a ... x] f(t) dt
Soit G une primitive de f alors il existe k réel tel que :

F(x)=G(x)+k

en gros démontrer que F est UNE primitive de f.

[Alpha]

Oui, en gros tu veux partir de la définition de l'intégrale avec les fonctions en escalier, ie comme l'aire entre la courbe et l'axe des abscisses, et démontrer que cette aire entre a et b vaut l'intégrale de a à b de la fonction...

[Skullkid]

Bonjour, tu dois montrer que la fonction F définie par est dérivable et que F' = f.

Pour ça tu dois considérer un élément quelconque de l'intervalle I sur lequel f est conitnue, et montrer que . Je crois qu'on est obligé de passer par la définition formelle de la limite mais je n'ai plus la démo exacte en tête...si tu veux je peux resortir mon cours. ^^

@Alpha : je crois pas qu'on ait besoin des fonctions en escalier ici, l'intégrale est déjà construite.

[quinto]

C'est une conséquence presqu'immédiate du théorème de la valeur moyenne.

Le problème est que pour réussir à montrer ce que tu veux, tu vas devoir passer par pas mal de résultats intérmédiaires.

[Alpha]

@Alpha : je crois pas qu'on ait besoin des fonctions en escalier ici, l'intégrale est déjà construite.

Je disais pas qu'on en avait besoin, mais que c'est à partir de cette construction-là de l'intégrale qu'on montrait le lien avec les primitives.

[Skullkid]

Oui en effet, désolé j'avais mal compris...

[lapras]

Quinto :
je ne connais pas ton théoreme de la valeur moyenne,
par contre je connais la définition :
On appelle valeur moyenne de f sur [a;b] le nombre k tel que int [a...b] f(t) dt = k(b-a)

si je traduis ceci géométriquement k est le nombre réel pour lequel l'aire du rectangle de largeur k est égale à l'aire de la partie du plan limitée par la courbe de f.

C'est a partir de cette définition que tu veux que je le prouve ?


EDIT :
Plus loins dans le cour il y a ce théoreme, mais je souhaite démontrer le théoreme admis sans les théoremes qui en découlent plus tard dans le cour !

[oscar]

Bonjour

Voici une démo trouvée dans mon livre

http://img251.imageshack.us/img251/184/theormesurlesprimitivesbc8.jpg

[Nightmare]

Bonjour.

On veut montrer que la fonction F définie par avec f continue sur un segment [a,b] est l'unique primitive de f qui s'annule en a.

Occupons nous du taux d'accroissement :
par la relation de Chasles.

Or, f étant continue sur le segment [a,b], elle est bornée et atteint ses bornes. On note M=sup f et m= inf f.

On a alors pour tout x,

Et donc d'après l'inégalité de la moyenne :

et finalement :


Par conséquent, il existe d'après le Tvi un réel tel que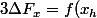

Et ainsi en faisant tendre h vers 0, xh tend vers x et comme f est continue :
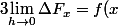CQFD.

[lapras]

Merci beaucoup, c'était beau :++:
Juste :
tu ne t'es pas trompé dans la démo au moment où tu écris :
d'apres l'inégalité de la moyenne : ....
ca serait plutot int[x ... (x+h)] noN ?

encore merci

[Nightmare]

Euh oui je corrige ça.

[lapras]

Autre chose :
Le théoreme des valeurs moyennes peut se démontrer grâce à ce théoreme, mais moi je le démontre intuitivement grâce a un dessin en faisant la moyenne de "l'aire".
je peux ?

[Nightmare]

Euh non, le théorème de la moyenne sert à démontrer le théorème fondamentale mais pas l'inverse.

En fait l'inégalité de la moyenne est simple :


En intégrant des deux côtés entre a et b :


Or, les intégrandes à gauche et à droites sont des constantes donc :
.
C'est l'inégalité de la moyenne.

Ensuite on se sert du TVI pour montrer le théorème de la moyenne.

[Sylar]

Ca ressembe au programme de Sup ça :hum:

Lapras ,tu vas faire une prépa ?