RadarX a écrit:Bonsoir mesdames mesdemoiselles messieurs,
(Meme si ce post est à l'intention de farh et de BQSS)
mon premier post a bien commencé par un bonjour et ai utilisé une formule assez courtoise . Il y a donc eu le minimum de correction conformement a ce qu'on requiert dans ce forum que je connais assez bien. Ce n'est, en effet, pas la premiere fois que je viens.
pour le deuxieme post, j'admet en effet ne pas avoir salué. Mais bon c'est parce que la discusion était lancée et cela arrive souvent qu'apres le 1er post d'un membre dans une meme discus, qu'il enchaine spontanement les suivants sans le bonjour.
Voila, cela dit, merci quand meme farh pour ta reponse; en fait j'ai reussi a le retrouver en refaisant la demo (utilisation de la jacobienne).
Merci aussi a BQSS meme si je reste pas d'accord; je t'envoie une demo de ce que j'affirme (enfin pas moi, du resultat) dès que j'ai fini. Il n'existe pas que des integrales sur compacts: il y a aussi des integrales generalisées.
Salut.
Mais evidemment qu'il y a des integrales generalisé.
Ce n'est pas la question. grrrrrrrrrr :marteau: .
T'es tetu hein.
C'est localement integrable sur R^3 ta question!!!!!
Ca veut dire integrable sur tout fermé!! Compact donc ici pour R^3!!
inclu dans
ce que toi tu as appelé R^3
Mais la c'est faux car sur tout les intervalles qui contiennent 0 ou tu vas integrer, il y aura un point non défini qui n'est pas sur la peripherie du compacte et tu ne pourras pas integrer sur le fermé [a;b]^3 par exemple car tout simplement pas défini sur un point inclu dans [a;b]^3 (et evidemment ici pas prolongeable par continuité).
On parle d'integrale genéralisé quand ce n'est pas défini sur une borne et dans ce cas on dit integrable sur [a;b[ et on
exclu la borne b.
Donc peu importe ta demo(je me fiche de ta demo, si tu cherches juste a calculer l'integrale généralisé sur R^3 privé de 0, le calcul est elementaire, c'est juste qu'elle ne repond pas a ta question, ce que tu cherches a démontré a mon avis c'est que c'est integrable et pas loc integrable qui veut dire autre chose sur toute boule fermée ou l'on a exclu l'origine, tu parles donc d'integrale généralisé et meme la donc il faut exclure l'origine car meme quand on parle d'integrale généralisé on défini un ouvert ou la fonction est defini, apres en spherique tu prends la limite quand r-->0 ) mais ce que tu demandes n'a pas de sens (sauf si tu exclus 0 , que tu parles de localement integrable ou d'integrale généralisé sur R^3 privé de 0, il faut exclure 0, de plus toi tu veux en fait calculer une integrale généralisée et ta question parle de localement integrable, deux choses differentes).
On ne defini pas une integrale sur un ensemble ou ce n'est pas defini.
Voila la definition de l'integrale impropre sur [a;b[
b excluSoit
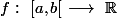
une fonction continue.
Si la limite
dt)
existe et est finie, on appelle cette limite intégrale impropre de f sur [a,b[.
On ne defini pas cette integrale ailleurs que l'a ou elle est defini, sauf que pour sa borne on cherche la limite, donc la on exclu 0, c'est quand meme pas compliqué.
1)Toi tu parles deja de
localement integrable, on parle donc de compacte(definition) inclu dans R^3 et tout ceux qui contienne 0 ne sont pas definie sur R^3!!! L'integrale généralisé n'a rien a voir ici, on integre que sur des compacte et une integrale genéralisé est par definition defini sur tout sauf un compacte...
2) deuxiemement ton integrale ne peut etre defini pour tout les intervalles d'integration qui contienne 0 tout simplement.
3)Quand bien meme 0 serait a la peripherie(donc en surface pour R*R*R\(0;0;0)) il faudrait exclure 0 car on ne parle pas d'integrale généralisé sur un fermé, ca n'a pas de sens(et on ne parlerait pas de localement integrable , mais juste d'une integrale impropre sur R*R*R\(0;0;0)) en coordonnée spherique r=0 est bien a la peripherie(on parlerait plus de R mais de R+* etoile deja en spherique pour r), mais il faut aussi exclure r=0 car integrale généralisé ou pas on ne defini que l'integrale la ou la fonction existe (r appartient à R+*). En spherique, meme probleme donc ce n'est pas defini pour r=0, on parlerait donc de localement integrable avec pour r definie sur R+*.
4)par contre si tu lisais bien, tu verrais que dans le premier post j'ai rappelé que c'etait bien localement integrable sur R*R*R privé de 0(qui est un ouvert), toujours rien avoir avec les integrales generalisé, puisqu'on parle de
localement integrable(la demonstration c'est ce que j'ai donné au 1) ).
5)Si tu veux parler d'integrale genéralisé, tu peux dire que c'est integrable(on ne parle plus de localement integrable mais d'autre chose) sur un tout ouvert inclu dans R^3\{0,0,0) (ce qui est autre chose qu'au 5). Mais ca n'a rien avoir avec ta question qui parle de localement integrable et qui parle de R^3 tout entier.
je te rappele que loc(R^3) ca veut dire localement integrable sur R^3.
6)Donc si tu veux parler juste d'integrable et pas de localement integrable, il faut premierement definir l'ensemble R*R*R\{0,0,0) et pas parler de R^3 tout entier, deuxiemement demander si c'est integrable et pas
localement integrable sur cet ensemble de R*R*R\{0,0,0) et pas sur R^3 tout entier et
ALORS , seuleument alors, ca voudra dire quelquechose.
7) Une fois que tu t'exprimes clairement, et que tu demandes le 6) et pas ton premier post qui ne veut rien dire, oui tu peux passer en coordonnée spherique et calculer l'integrale de 1/||x|| sur un ouvert inclu strictement dans R^3\{0,0,0) ou l'integrale généralisé d'un ouvert inclu dans R^3\{0,0,0) de "borne superieur scritement inferieur a +infini^3 si tu veux" en utilisant la limite quand r-->0 pour voir que ca admet bien une limite fini/
8)une fois passer en coordonée spherique: 1/||x||=1/r et donc la fonction ne depend plus que d'une variable et c'est triviale. On se retrouve a integrer apres changement de variable lim quand h-->0 integrale(rsin(a)dadrdo), avec r definie sur [h,p], soit en fait une integrable génralisé pour r definie sur ]0,p].
9)Mais attention a nouveau ce n'est pas integrable pour l'integrale géralisé definie pour r appartient à ]0,infini[ car l'integrale diverge en +infini! pour la variable r. Donc a nouveau ici on ne peut parler d'integrable sur R^3 privé de 0 (pour l'integrale génralisé) car cela diverge(pour r=0 pas de probleme mais en +infini il y a un probleme).
10)au final c'est du grand n'importe quoi
et la seule chose qui soit vrai et demontrable c'est que 1/||x|| est integrable (integrale généralisé) pour r definie sur ]0,p] ou ]0;p[ peu importe.
Et en spherique teta et phi ne sont pas definie sur R tout entier evidemment, mais on est plus a ca pres.
11)Finalement je resume, ce que tu peux demontrer c'est que 1/||x|| est integrable(et pas loc integrable) sur tout ouvert dont la borne superieur est strictement inferieur a +infini et privé de (0;0;0) (dans ce cas on utilise l'integrale impropre en (0;0;0). Pour demontrer ca une fois passé en coordonnée spherique la demonstration est elementaire(il suffit de connaitre la primitive de r et de prendre la limite quand r^2/2 tend vers 0 ensuite).
Ou tu peux dire (c'est autre chose) integrable sur tout fermé inclu dans R^3 privé de (0;0;0) soit localement integrable sur R^3 privé de (0;0;0) (comme je l'ai dit au premier post!!!!) (et pas sur R^3 tout entier, dans ce deuxieme cas l'integrale improrpre n'a rien a voir d'ailleurs)
Ce n'est pas une question de calcul(le calcul de cet integrale généralisée est primaire), mais de definition. Vu que localement ca veut dire pour tout ensemble inclu, si tu veux integrer sur [0;a] ce n'est pas défini en 0(c'est faux), pour la variable r qui est bien inclu dans [0;+infini[ (c'est la qu'est defini r), il faut ecrire ]0;a](on exclu la borne) et dans ce cas c'est une integrale généralisé.
Si tu parles de localement la c'est meme plus une question d'integrale génralisé, on s'attaque a des compactes,et la aussi il faut exclure r=0 ou ce n'est pas defini.
Bon ce n'est pas dirigé specialement contre toi mais je vais prendre un peu congé du forum car c'est fatiguant les gens tetu a qui il faut repeter plusieurs fois les memes choses. J'ai beaucoup de boulot et se justifier pour ce qui devrait etre evident ou expliquer encore et encore a quelqu'un qui ne veut pas comprendre me prend trop de temps. Je trouve ca fort que de polemiquer ou de ne pas etre d'accord avec un niveau qui n'est plus la (ou je ne parle pas pour toi qui n'a jamais été). Ca a le dont de m'agacer, oser dire "il y a aussi les integrales generalisé"(niveau premier année post bac) comme si quelqu'un qui repondait sur les compacts(on voit les compacts avant les integrales impropres maintenant, tiens dont) n'avait pu voir cette notion et comme si c'etait la notion ultime(qui d'autre que quelqu'un qui a oublié l'essentiel des notions mathematiques prendrait le besoin de le rappeler me dirait vous, quelqu'un qui ne se souvient pas que c'est une notion elementaire), avouer qu'on a plus le niveau puis tout de meme foncer droit dans le mur et refuser de comprendre ce qu'on lui explique en clamant qu'on est en desaccord de surcroit c'est orripilant et en plus ca me fait perdre un temps fou. Si moi je me mettais a contesté un jury de 5 medaille fields sur la geometrie algebrique ce serait du meme genre, toi qui me rappelle alors que je
prends le temps de te repondre, qu'il y a aussi les integrales impropre alors que tu racontes n'importe quoi et que tu n'as "plus" je t'accorde le plus aucune notion ca m'exaspere.
A+ les amis, je reviendrai d'ici mes exams, faire quelques tours ou eventuellement participer a un ou deux trois defis.
A+ fahr, Yos, Imod, Sadrine et les amis
