Sous groupes d'un groupe cyclique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
murray
- Membre Naturel
- Messages: 84
- Enregistré le: 17 Mai 2006, 17:50
-
 par murray » 24 Aoû 2007, 17:20
par murray » 24 Aoû 2007, 17:20
bonsoir,
je voudrais savoir si les sous-groupes d'un groupe cyclique sont eux-mêmes cycliques.
Merci pour votre aide.
M.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 24 Aoû 2007, 17:53
par kazeriahm » 24 Aoû 2007, 17:53
il me semble bien que oui
cherche sur wikipédia pour une démo
-
ulmo
- Messages: 8
- Enregistré le: 20 Aoû 2007, 21:55
-
 par ulmo » 24 Aoû 2007, 21:36
par ulmo » 24 Aoû 2007, 21:36
Bonsoir,
Un groupe cyclique

est un groupe généré par un unique élément nilpotent (c'est donc un groupe fini).
Autrement dit, si

est un groupe généré par

nilpotent d'ordre

, il est constitué des éléments

avec

.
Or tout élément de

différent de l'élément neutre suffit à générer

tout entier.
Donc les seuls sous-groupes de

sont les sous-groupes dits triviaux ,soit
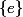
et

, qui sont eux mêmes bien sûr cycliques.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 24 Aoû 2007, 21:45
par kazeriahm » 24 Aoû 2007, 21:45
salut
bah non c'est faux parce que dans (Z/nZ,+) avec n non premier, si p est un entier non premier avec n, alors la classe de p n'engendre pas Z/nZ tout entier
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 24 Aoû 2007, 22:12
par fahr451 » 24 Aoû 2007, 22:12
bonsoir
un groupe cyclique d'ordre n admet pour tout d diviseur de n un unique sous groupe d'ordre d ( qui est cyclique)
-
ulmo
- Messages: 8
- Enregistré le: 20 Aoû 2007, 21:55
-
 par ulmo » 24 Aoû 2007, 22:13
par ulmo » 24 Aoû 2007, 22:13
euh ... en effet.
Mon cas ne fonctionne alors que si

est premier
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 24 Aoû 2007, 22:25
par kazeriahm » 24 Aoû 2007, 22:25
fahr451 a écrit:bonsoir
un groupe cyclique d'ordre n admet pour tout d diviseur de n un unique sous groupe d'ordre d ( qui est cyclique)
that's it! et les sous groupes de G ont pour cardinal un diviseur de n donc ils sont tous cycliques
-
murray
- Membre Naturel
- Messages: 84
- Enregistré le: 17 Mai 2006, 17:50
-
 par murray » 25 Aoû 2007, 16:29
par murray » 25 Aoû 2007, 16:29
OK c'est bien ce que je pensais. Merci à tous pour votre contribution
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
 est un groupe généré par un unique élément nilpotent (c'est donc un groupe fini).
est un groupe généré par un unique élément nilpotent (c'est donc un groupe fini). est un groupe généré par
est un groupe généré par  nilpotent d'ordre
nilpotent d'ordre  , il est constitué des éléments
, il est constitué des éléments  avec
avec  .
. différent de l'élément neutre suffit à générer
différent de l'élément neutre suffit à générer  tout entier.
tout entier. sont les sous-groupes dits triviaux ,soit
sont les sous-groupes dits triviaux ,soit 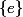 et
et  , qui sont eux mêmes bien sûr cycliques.
, qui sont eux mêmes bien sûr cycliques.