Eq diff

[zorg]

Le 5 août, je demandais une aide sur ce forum pour l'eq. diff suivante:

y''+|y|=1 et y(0)=0 et y'(0)=1

mais je n'ai reçu aucune réponse satisfaisante. Ayant réfléchi au problème depuis, je vous livre mes réflexions...

On considère les problèmes de Cauchy suivants:

dont l'unique solution est

dont l'unique solution est et

dont l'unique solution est

Soit à présent f une solution sur R de (E). f est au moins de
classe C^2 car f''=1-|f|.

f'(0)=1 donc par continuité de f' en 0, f'>0 sur un voisinage
de 0 donc f est strictement croissante un voisinage de 0. Comme
f(0)=0, f>0 à droite de 0 et f<0 à gauche de 0 (localement).

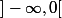
Supposons que f s'annule sur . Notons la valeur d'annulation telle que f ne s'annule pas sur . Alors la restriction g de f à garde un signe constant (fonction
continue ne s'annulant pas sur un intervalle). Comme f<0 à gauche de
0, g est une fonction négative donc elle vérifie le problème de
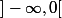
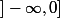
Cauchy . Par unicité on a donc , . Or la fonction ne peut s'annuler en (qui est <0) donc il y a une contradiction. Donc f ne s'annule pas sur donc f est négative sur et donc vérifie le problème de Cauchy donc , .

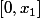
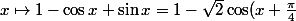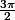
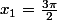
Supposons à présent que f s'annule sur en et que soit la première valeur d'annulation strictement positive. Par un raisonnement analogue au paragraphe précédent, la restriction h de f à vérifie le problème de Cauchy et donc , . Or la fonction s'annule la première fois en . Donc et , . En particulier f vérifie et . Par un raisonnement
déjà fait, on en déduit que f est strictement négative à droite
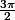
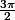
(localement) de . On montre alors (raisonnement déjà fait) que f ne peut s'annuler au delà de donc f vérifie le problème de cauchy . Conclusion:

(E) admet une unique solution qui est: