Forme indeterminée fonction trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
solo_vulkan
- Messages: 1
- Enregistré le: 23 Aoû 2007, 14:27
-
 par solo_vulkan » 23 Aoû 2007, 14:30
par solo_vulkan » 23 Aoû 2007, 14:30
lim en +inf de x²-x³sin(1/x)
quelqu'un aurait il une idée?
Merci
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 23 Aoû 2007, 14:41
par Sylar » 23 Aoû 2007, 14:41
solo_vulkan a écrit:lim en +inf de x²-x³sin(1/x)
quelqu'un aurait il une idée?
Merci
En 0 : sin(x) /x -> 1
(1/x) -> 0 => lim[sin(1/x)}=lim 1/x
lim [ x²-x³sin(1/x) ] = 0
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Aoû 2007, 14:57
par Skullkid » 23 Aoû 2007, 14:57
Ça tend vers 1/6...mais pour l'instant je ne vois pas comment le démontrer sans utiliser de DL.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 23 Aoû 2007, 14:59
par kazeriahm » 23 Aoû 2007, 14:59
mm ca manque de rigueur sylar tout ca, tu utilises un équivalent donc c'est juste mais ce que tu marques c'est faux
c'est comme si tu disais
(1+1/n)^n ? 1+1/n tend vers 1 en l'infini donc la limite rechercée est 1.... ce qui est faux
ici on a une forme indeterminée...
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 23 Aoû 2007, 14:59
par kazeriahm » 23 Aoû 2007, 14:59
bah non ca tend vers 0...
-
marie49
- Membre Relatif
- Messages: 180
- Enregistré le: 06 Aoû 2007, 15:48
-
 par marie49 » 23 Aoû 2007, 15:00
par marie49 » 23 Aoû 2007, 15:00
en faisant un changement de variables X=1/x dans xsin(1/x)
en fait on voit que xsin(1/x)=sin(1/x)/(1/x)
et 1/x tend vers 0 en +inf
donc tu retrouves lim sin(X)/X en 0, qui est egale a 1
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 23 Aoû 2007, 15:02
par kazeriahm » 23 Aoû 2007, 15:02
bah oui mais pendant ce temps... l'autre terme tend vers +l'infini
je vois pas comment faire sans DL
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 23 Aoû 2007, 15:05
par Sylar » 23 Aoû 2007, 15:05
Ca tend vers 0 .....
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Aoû 2007, 15:05
par Skullkid » 23 Aoû 2007, 15:05
kazeriahm a écrit:bah non ca tend vers 0...
=x^2-x^3 \left( \frac1x - \frac1{6x^3} + o \left( \frac1{x^3} \right)\right) = x^2-x^2+\frac16+o(1) \to \frac16)
Où est mon erreur ?
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 23 Aoû 2007, 15:06
par Sylar » 23 Aoû 2007, 15:06
Ah j'ai aditionné les équivalents :triste:
-
marie49
- Membre Relatif
- Messages: 180
- Enregistré le: 06 Aoû 2007, 15:48
-
 par marie49 » 23 Aoû 2007, 15:09
par marie49 » 23 Aoû 2007, 15:09
l'erreur provient du fait que tu a fait une partie de ton dl en 0 et l'autre en +inf
-
marie49
- Membre Relatif
- Messages: 180
- Enregistré le: 06 Aoû 2007, 15:48
-
 par marie49 » 23 Aoû 2007, 15:10
par marie49 » 23 Aoû 2007, 15:10
c'est vrai que sans les DL et les equivalents c'est pas évident de répondre a la question
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Aoû 2007, 15:12
par Skullkid » 23 Aoû 2007, 15:12
marie49 a écrit:l'erreur provient du fait que tu a fait une partie de ton dl en 0 et l'autre en +inf
J'ai fait mon DL en 1/x, donc en 0...
-
marie49
- Membre Relatif
- Messages: 180
- Enregistré le: 06 Aoû 2007, 15:48
-
 par marie49 » 23 Aoû 2007, 15:18
par marie49 » 23 Aoû 2007, 15:18
oui, mais pour faire ton dl en 0, tu as fait un changement de variables u=1/x, qui tend bien vers 0 qd x tend vers +inf.
mais, n'oublie pas que dans ce cas, ton x^2 devient 1/u^2 et ton x^3 devient 1/u^3. ce n'est pas un dl, donc tu n'as pas le droit de multiplier les deux termes x^2 et (1/x etc..)
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 23 Aoû 2007, 15:19
par Sylar » 23 Aoû 2007, 15:19
Oui je suis d'accord ,t'as une partie en 0 ,l'autre en +inf .....
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Aoû 2007, 15:23
par Skullkid » 23 Aoû 2007, 15:23
Je ne vois toujours pas le problème, si je recommence avec u=1/x :
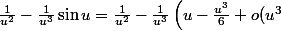\right)=\frac1{u^2}-\frac1{u^2}+\frac16+o(1)\to \frac16)
-
marie49
- Membre Relatif
- Messages: 180
- Enregistré le: 06 Aoû 2007, 15:48
-
 par marie49 » 23 Aoû 2007, 15:28
par marie49 » 23 Aoû 2007, 15:28
un DL en 0 est une expression polynomiale en u c'est à dire une expression de la forme a'0'+a'1'u+a'2'u^2 etc... donc 1/u^3 n'est pas un DL.
tu ne peux pas multiplier une expression quelconque en u avec un DL, il faut que ce soient deux DL.
pour les memes raisons tu ne peux pas les additionner. c'est pour ca que tu trouves un résultat faux
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 23 Aoû 2007, 15:34
par kazeriahm » 23 Aoû 2007, 15:34
non mais en fait c'est juste ca tend bien vers 1/6 desolé sullkid
je vois pas le problème marie et sylar
un développement limité c'est une égalité
sin(1/x)=1/x-1/6*x^3+o(1/x^3)
donc on trouve bien 1/6+o(1)
-
marie49
- Membre Relatif
- Messages: 180
- Enregistré le: 06 Aoû 2007, 15:48
-
 par marie49 » 23 Aoû 2007, 15:41
par marie49 » 23 Aoû 2007, 15:41
houla, ca m'a perturbé cette histoire, c'est vrai t'as raison en fait.
je sais pas pourquoi mais au début quand j'ai fait le calcul j'ai fait une erreur et j'ai trouvé 0, puis après je suis restée dans mon idée et j'ai dit des grosses bétises.
au temps pour moi
vraiment désolée!
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 23 Aoû 2007, 15:44
par Skullkid » 23 Aoû 2007, 15:44
C'est pas grave, ça peut arriver à tout le monde ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
