Inéquation du premier degrés

par **cactus-32** » 19 Aoû 2007, 13:44

Chers membres,
bonjour,
je passe en première Scientifique et j'ai des devoirs pour la rentrée j'ai tout fais
sauf cette équation dont je ne trouve pas de réponse cohérente:
(2x-5)(-x-3)<-15
merci d'avance pour toute solution.
cordialement.

par **lapras** » 19 Aoû 2007, 13:46

Bonjour !
Il faut développer, réduire, passer le -15 de "l'autre côté", obtenir un polynome du second degré, calculer les racines, utiliser les théoremes sur le signe du trinome !EDIT : as tu vu la résolution du second degré en seconde ? Si non, ca risque d'etre un peu dure avec ma méthode !

par **cactus-32** » 19 Aoû 2007, 13:50

je n'ai étudier malheureusement que le premier degrés

par **lapras** » 19 Aoû 2007, 13:53

Sinon tu peux la résoudre graphiquement :)
Es tu sur que c'est bien < -15 ?
et non <0 ?
Dans ce cas c'est un tableau de signe qu'on aurait pu faire

par **cactus-32** » 19 Aoû 2007, 13:56

c'est <-15 donc il faut faire un graphique avec quelle équation de droite?
d'avance merci beaucoup

par **anima** » 19 Aoû 2007, 13:56

cactus-32 a écrit:Chers membre,
bonjour,
je passe en première Scientifique et j'ai des devoirs pour la rentrée j'ai tout fais
sauf cette équation dont je ne trouve pas de réponse cohérente:
(2x-5)(-x-3)<-15
merci d'avance pour toute solution.
cordialement.

Moi, je parie sur un +15 au lieu de -15, comme ca, on aurait +15 de chaque coté, et on retomberait sur une inéquation du style ax^2+bx<0

Il n'y a pas d'équation de droite; c'est une équation d'une parabole que tu auras...

par **lapras** » 19 Aoû 2007, 13:59

Moi aussi je parie sur +15

par **cactus-32** » 19 Aoû 2007, 14:32

j'ai vérifier et sur l'énoncé malheureusement c'est -15
alors que faire?
merci pour vos réponses.

par **lapras** » 19 Aoû 2007, 14:34

Je pense qu'il va falloir que t'apprennes la résolution des équations du second degré :ptdr:
Ca t'avancera pour la premiere :)

Déjà, sais tu factoriser sous forme canonique ?

par **cactus-32** » 19 Aoû 2007, 14:37

non
pourrais-tu m'expliquer s'il te plaît
merci :)

par **lapras** » 19 Aoû 2007, 14:41

je suis pas un tres bon prof, mais par contre tu peux aller sur google : "équation du second degré" et tu auras un line vers wikipédia.

par **cactus-32** » 19 Aoû 2007, 14:43

ok merci quand même pour ton aide

par **lapras** » 19 Aoû 2007, 14:45

de rien et si tu as un probleme, pose le sur le forum, on sera la pour t'aider ! :happy2:

par **anima** » 19 Aoû 2007, 14:50

[quote="cactus-32"]Chers membres,
bonjour,
je passe en première Scientifique et j'ai des devoirs pour la rentrée j'ai tout fais
sauf cette équation dont je ne trouve pas de réponse cohérente:
(2x-5)(-x-3) 0, on essayera de faire apparaitre (a+b)^2, sinon (a-b)^2. On se retrouvera avec un reste, noté r, qu'on soustrait par la suite. On aura donc

... ssi |x+a| =

.

2 racines. Ensuite, on applique le théoreme dit du signe du trinome.

Methode 2, dite du discriminant: dans une équation de la forme ax^2+bx+c=0, on pose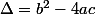

.
Si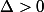

, l'équation possede 2 racines réelles:

et

Si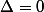

, l'équation possede une racine double réelle:

(forme cannonique parfaite)
Enfin, si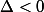

, tu verras en terminale que l'équation admet 2 racines, mais qu'elle n'appartiennent pas au domaine des réels.

par **cactus-32** » 19 Aoû 2007, 14:56

j'obtient après avoir développé :
-2x²-x+30<0 c'est donc une inéquuation du second degrés?

par **anima** » 19 Aoû 2007, 14:58

cactus-32 a écrit:j'obtient après avoir développé :
2x²-x+30<0 c'est donc une inéquuation du second degrés?

Perso, je trouve -2x^2-x+30...

Enfin, oui, c'est une inéquation du second degré. Pour la résoudre:
- On trouve les racines de -2x^2-x+30 avec la méthode que tu préferes
- On en déduit le signe de -2x^2-x+30 sur

- On résout! :zen:

par **cactus-32** » 19 Aoû 2007, 15:02

pourquoi chercher les racines de -2x²-x+30?
je ne comprend pas

par **lapras** » 19 Aoû 2007, 15:03

Parce qu'en trouvant les racines de ce trinôme du secon degré, tu pourras utiliser un théoreme qui dit que pour tout x entre les racines, alors le signe de f(x) est le signe contraire de a.

par **anima** » 19 Aoû 2007, 15:04

lapras a écrit:Parce qu'en trouvant les racines de ce trinôme du secon degré, tu pourras utiliser un théoreme qui dit que pour tout x entre les racines, alors le signe de f(x) est le signe contraire de a.

Et ca se dit aimer les démonstrations? Je suis choqué, la :doh:

On cherche les racines car un polynome est une fonction continue, donc un polynome ne peut changer de signe sans s'annuler :we:

par **cactus-32** » 19 Aoû 2007, 15:05

donc je fais racine de (2x²-x+30)?

Inéquation du premier degrés

inéquation du premier degrés

Qui est en ligne