Bonsoir,
voila un exercice d'olympiade si certains veulent y réfléchir:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 ...
Une ligne est désignée par le nombre écrit dans la première case à gauche.
Une colonne est désignée par le nombre écrit dans sa case la plus haute.
Par exemple, le nombre 11 est repéré par (10,5), le nombre 8 par (5,4).
Comment est repéré le nombre 2003 ?
Olympiade
9 messages
- Page 1 sur 1
par alben » 06 Aoû 2007, 22:53
problème d'espaces qui ne sont pas pris en compte dans l'affichage. Il t'aurait fallu mettre des points au lieu d'espace et choisir une police courrier
[FONT=Courier New]
..... ... 1
..... 2.. 3 4
... 5 6.. 7 8 9
10 11 12 13
[/FONT]
[FONT=Courier New]
..... ... 1
..... 2.. 3 4
... 5 6.. 7 8 9
10 11 12 13
[/FONT]
par Imod » 06 Aoû 2007, 23:07
Ca n'a pas l'air trop difficile en remarquant que la pente à droite donne les carrés des entiers , ou alors j'ai raté l'essentiel .
Imod
Imod
par Imod » 06 Aoû 2007, 23:19
Si ^2)
, l'abscisse de 
est 
. Ca semble quand même un peu plus délicat pour l'ordonnée .
Imod
Imod
par Imod » 07 Aoû 2007, 09:58
Une méthode pas très jolie mais qui marche bien sur des petits nombres comme 2003 .
[TEX]44^2 1937 et 529 ( sauf erreur ) .
Imod
[TEX]44^2 1937 et 529 ( sauf erreur ) .
Imod
par Bouchra » 08 Aoû 2007, 22:28
Salut,
Pour le cas général:
pour l'ordonnée, je représente chaque colonne par une suite)
avec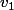 
de la forme 
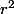ou ^2+1)
.
Pour une colonne donnée où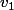 est de la forme 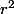ou ^2 + 1)
, on a :
)
..
)
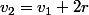
en sommant on obtient :
 r + (p-1)(p-2))
(*)
Soit
un entier naturel non nul dont on cherche la représentation.
il existe un unique n entier naturel tq :^2 n)
alors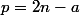 
.
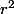L'ordonnée de est de la forme dans le second cas, et de la forme dans le premier cas.
D'après (*), on résoud pour
: r+(p-1)(p-2))
, (ici p=
)
Après simplifications:
, d'où :
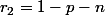
pour
, on résoud : ^2+1+2(p-1)r+(p-1)(p-2))
, (ici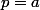 
)
^2)
Récapitulons:
Soit entier naturel non nul.
Si^2 + a)
avec alors est représenté par le couple :
^2+1, (a-n+1)^2))
- Si alors k est représenté par :
^2+1,(n-a)^2+1))
Pour le cas général:
pour l'ordonnée, je représente chaque colonne par une suite
Pour une colonne donnée où
..
en sommant on obtient :
Soit
il existe un unique n entier naturel tq :
L'ordonnée de
D'après (*), on résoud pour
Après simplifications:
pour
Récapitulons:
Soit
Si
- Si
par Bouchra » 09 Aoû 2007, 11:55
Bon en fait on peut trouver l'ordonnée sans tous ces calculs:
Si a>n, k=v_p avec p=2n-a
extrémité à droite 
extrémité à droite ^2)
...
})
extrémité à droite)^2=(a-n+1)^2=v_1)
de même si
.
Si a>n, k=v_p avec p=2n-a
...
de même si
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :