Probabilité

par **mariounette** » 06 Aoû 2007, 22:21

Bonjour à tous,

Lorsque l'on décompose une fonction de repartition en une fonction de repartition d'une mesure purement atomique et une f de r continue, apparemment ça peut s'écrire

. avec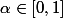

. Je ne comprends pas le

. Pour moi ça s'écrirais simplement

.

par **Pouick** » 07 Aoû 2007, 10:57

Bin j'ai trouvé que ca pouvait s'ecrire F=

où

page en question

par **HAL 9000** » 07 Aoû 2007, 15:35

Le

vient tout simplement du fait que la fonction de répartition prend ses valeurs entre 0 et 1... rien de plus ! Si tu ne mets pas de coefficient

cela veut dire que sa valeur est toujours 1 sur R, ce qui n'est pas toujours le cas (en pratique rarement meme)...

par **mariounette** » 07 Aoû 2007, 17:02

oui F est compris entre 0 et 1 mais F_{atom} aussi et F_{cont} aussi. F_{cont}(t) c'est juste F(t) privé du poids des atomes qui sont avant t, donc en rajoutant F_{atom}(t) je rajoute le poids des atomes qui se trouvent avant t et je récupère F(t). Je n'ai rien compris ?

par **HAL 9000** » 07 Aoû 2007, 17:24

Je t'explique : la fonction de répartition est selon l'étude soit discontinue (cas d'un variable aléatoire mesurable par rapport à la mesure de Dirac c'est-à-dire discrète) soit continue (cas d'une variable aléatoire mesurable par rapport à la mesure de Lebesgue). Ainsi pour ecrire la fonction de répartition englobant ces deux cas, on écrit :

F(t) = alpha (F(t) * mesure de Dirac en t + F(t) * mesure de Lebesgue en t)
ou alpha est compris entre 0 et 1.

c'est-à-dire :

Probabilité

probabilité

Qui est en ligne