Controles 1ere S

par **anima** » 30 Juil 2007, 20:39

Je ne pense pas, les 3 sont des suites.

par **kuid312** » 30 Juil 2007, 20:39

:salut:

Point d'inflexion veut dire quoi? :look2:

Merci :++:

par **anima** » 30 Juil 2007, 20:40

kuid312 a écrit::salut:

Point d'inflexion veut dire quoi? :look2:

Merci :++:

Un point ou la concavité de la courbe change; si tu préfere, si la ventre fait un creux ou une bosse :p

par **lapras** » 30 Juil 2007, 20:42

OUPS désolé anima, en fait je n'avais pas capté que c'était un "controle" que tu me passais, je le voyais sous forme de polycopié, c'est pour ca , encore désolé, je vais faire ca immédiattement.

par **anima** » 30 Juil 2007, 20:43

lapras a écrit:OUPS désolé anima, en fait je n'avais pas capté que c'était un "controle" que tu me passais, je le voyais sous forme de polycopié, c'est pour ca , encore désolé, je vais faire ca immédiattement.

Je ne t'ai pas refilé un de "mes" controles, mais un sujet que j'ai corrigé ici-meme. :zen:

par **kuid312** » 30 Juil 2007, 20:52

Ok donc si j'ai compris, pour un trinome du second degré de la forme f(x)=ax²+bx+c (a diff de 0) Le point d'inflexion de Cf est le point d'abscisse -b/2a ?? : D

Question subsidiare (idiote): c'est la même chose si la courbe de ma fonction fait une bosse ou un creux?La courbe a-t-elle la même "appellation"?

Merci de l'info :happy:

par **lapras** » 30 Juil 2007, 21:05

J'ai tenté ceci :
Pour démontrer que la somme des entiers consécutifs de 1 + 2 +...+ n = n(n+1)/2 il y a deux méthodes :
Soit S = 1 + 2 +...+ n
on remarque 1 + 2 +...+ n + (n + (n- 1) + ... 1) = n(n+1)
donc que 2S = n(n+1) donc que S = n(n+1)/2
deuxieme possibilité :
On prend un rectangle, on détermine sa longueur à n+1 , sa largeur à n , l'air est de n(n+1)
l'air du triangle rectangle formé par la diagonale est égale à la moitié del'aire du rectangle soit n(n+1)/2
Voici un triangle formé a l'aide de caracteres ASCII :
.
..
...
....
.....

on remarque que son air en terme de points ets de 1 + 2 +3 +4 + 5
la somme de 1 + ... + n est donc de n(n+1)/2

Démonstration de :
2^0 + ... + 2^n = 2^(n+1) - 1 :
On vérifiée au rang n = 0 :
2^1 - 1 = 1 = 2^0
la propiété est vraie pour n = 0
montrons que la propriété eest vraie pour n+1 :
Il faudrait donc montrée que
2^(n+2) - 1 = 2^0 + ... + 2^(n+1)
donc que
2^(n+1) * 2 = 2^0 + ... + 2^(n+1) + 1
Posons A = 2^0 + ... + 2^(n+1) + 2^0
Simplifions A :
A = 2^1 + 2^1 + ... + 2^(n+1)
A = 2 * 2^1 + 2^2 + ... + 2^(n+1)
A = 2 * 2^2 + 2^3 + ... + 2^(n+1)
on arrive finalement a simplifier A :
A = 2 * 2^(n+1)
Donc
2^(n+1) * 2 = A = 2^0 + ... + 2^(n+1) + 1
donc
2^(n+1) * 2 - 1 = 2^0 + ... + 2^(n+1)
donc
2^(n + 2) - 1 = 2^0 + ... + 2^(n+1)

On a démontré que la propriété était vraie au rang n+1, par récurrence on a prouvé que 2^(n+1) - 1 = 2^0 + ... + 2^n.

J'ai aussi une autre méthode, mais eventuellement si celle ci est bonne, je ne la poste pas.
je ne suis abolument sur de rien !
merci de me corriger

par **B_J** » 30 Juil 2007, 22:45

Salut;
limites :

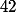
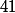
rep.

suites :
1)On considere la suite

definie par

1°montrer en raisonnant par recurrence que cette suite est majorée par le nombre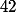

.
2°montrer que

En deduire que la suite

converge vers

.
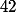2)La somme des termes d'une suite finie d'entiers impairs consecutifs ( positifs ou negatifs ) est egale a

.Quels sont les termes de cette suite ?
3)Determiner une progression geometrique contenant cinq termes reels , telle que :
1° la somme des trois premiers termes de la progression soit egale a

2° la somme des trois derniers termes de la progression soit egale a

4)

etant un nombre positif different de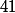

, on considere la suite de nombres

definie par la relation de recurrence

avec

on pose

1°montrer qu'il est possible de determiner 4$b de telle facon que la suite

soit geometrique
2°calculer 4$u_n en fonction de

et

.
bon courage :space:

par **lapras** » 30 Juil 2007, 22:48

je ferais tout ca demain, merci de ne pas donner la réponse (ou alors en blanc) pour la partie "suites" de tes exos.

par **B_J** » 30 Juil 2007, 22:50

lapras a écrit:je ferais tout ca demain, merci de ne pas donner la réponse (ou alors en blanc) pour la partie "suites" de tes exos.

ok , si t'as besoin d'un indice n'hesite pas :id:

par **Sylar** » 31 Juil 2007, 03:21

Je sens que tu vas cartonner a la rentrée lapras :) ......... :zen:

par **anima** » 31 Juil 2007, 08:52

lapras, si tu veux, je te donnerai tout ce qu'il me reste de l'an dernier en exos des que je rentre chez moi (mardi). Y'aura des suites, des complexes, peut-etre meme un véritable examen de 1ere S en maths avancés ;D

par **B_J** » 31 Juil 2007, 09:48

anima a écrit:lapras, si tu veux, je te donnerai tout ce qu'il me reste de l'an dernier en exos des que je rentre chez moi (mardi). Y'aura des suites, des complexes, peut-etre meme un véritable examen de 1ere S en maths avancés ;D

les complexes en 1ere ?

par **lapras** » 31 Juil 2007, 10:02

salut,
merci anima c'est sympa.
B J > pour tes exos sur les suites, j'avoue que j'ai un peu de mal !
Déja pour l'exo avec la somme de nombres impairs consécutifs est égal à 7^3 , j'ai cherché la somme d'une suite Un = 2n + 1 et j'arrive a la fin avec une équation a deux inconnues : U0 et n, l'important est de trouver U0 en premier il me semble, j'ai meme essayé avec quelques valeurs : avec 1 cela ne marche pas, ni avec 3 ...
Puis je avoir un indice ?

par **B_J** » 31 Juil 2007, 10:16

Salut Lapras ;
si x est le premier terme de la suite et n le nombre de termes qu'elle contient , comment s'exprime la somme recherchée en fonction de x et de n sachant que ces termes sont impairs et consecutifs?

par **anima** » 31 Juil 2007, 10:18

B_J a écrit:les complexes en 1ere ?

Programme européen. On a aussi fait pas mal de trucs que les francais n'ont pas fait, pareil pour la terminale (D.L., résolution d'équas diff a coeffs non-constants, et linéaires du second ordre, complexes appliqués a la géométrie, et un peu d'intégration poussée)...

par **lapras** » 31 Juil 2007, 10:22

Soit S cette somme :
S = x + (x +2*1) + ... + (x + 2*n)
S = x(n+1) + 2(1+2+...+n)
S = x(n+1) + n(n+1)
S = (n+1)(x + n)

par **B_J** » 31 Juil 2007, 10:25

anima a écrit:Programme européen. On a aussi fait pas mal de trucs que les francais n'ont pas fait, pareil pour la terminale (D.L., résolution d'équas diff a coeffs non-constants, et linéaires du second ordre, complexes appliqués a la géométrie, et un peu d'intégration poussée)...

c'est a peu pres ce qu'on a fait en terminale nous aussi , sauf les DL :we:

par **B_J** » 31 Juil 2007, 10:31

lapras a écrit:Soit S cette somme :
S = x + (x +2*1) + ... + (x + 2*n)

de 0 a n il y a n+1 termes
S=x + (x +2*1) + ... + [x + 2*(n-1)]

par **lapras** » 31 Juil 2007, 10:40

Oui mais en fait n termes pour moi c'est les n premiers termes sans le terme numéro 0
ex :
n=4 :
S = x + (x +2) + (x + 4) + (x+ 6) + (x+8)
Pour x =1
S = 1 + 1 + 2+ 1 + 4+ 1 + 6 + 1 + 8 = 25
Et
(n+1)(x + n) = (4+1)(4+1) = 25
Tu as raison je dois etre plus rigoureux je refais le calcul :
S=x + (x +2*1) + ... + x + 2*(n-1)
S = nx + 2(1 +...+(n-1)) = nx+(n-1)n = n(x+(n-1))

je dois maintenant résoudre :
n(x+(n-1)) = 7^3

Controles 1ere S

Qui est en ligne