Produit

[legeniedesalpages]

Bonsoir, voilà mon problème:

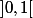
Soit une suite de points de , et soit une autre suite définie telle que



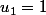
et pour tout entier n :

.

Je cherche à étudier la nature de la suite , plus précisément à trouver une (voire des) CNS sur sa convergence, mais je ne vois pas comment les trouver.

Merci pour votre aide.

[Joker62]

Comme ça en voyant un peu la forme je dirais d'étudier w_n = ln(u_n)
Donc transformation du produit en somme.

[BQss]

Salut,

Comme Joker a indiqué:
tu passes au log comme ça:
et est une suite a termes positifs.

Les cas:

soit ne tend pas vers 0 et la serie de termes diverge et donc converge vers 0 car en - l'infini l'exponentielle tend vers 0.

soit tend vers 0 et alors cette suite est équivalente a et donc plusieurs cas suivant la manière dont tend vers 0.
On compare a la serie de reference .
Si la serie diverge (i.e équivalente à un 1) et le tout tend vers une limite fini avec l la limite de la serie .


Dans tout les cas ca converge.

[legeniedesalpages]

On compare a la serie de reference .
Si la serie diverge (i.e équivalente à un <=1) alors le tout tend vers 0(idem qu'au 1).

Salut, je vois le canevas mais je ne me rappelle plus ce résultat sur les séries, en quoi le fait que la série diverge entraîne qu'il existe un réel tel que ~ ?

[BQss]

Salut, je vois le canevas mais je ne me rappelle plus ce résultat sur les séries, en quoi le fait que la série diverge entraîne qu'il existe un réel tel que ~ ?

C'est la réciproque qui est vrai, toute serie n'est pas équivalente à un c'était juste une manière d'analyser ta suite et d'itentifier si les converge, pour differencier les cas, l'idée c'est juste de savoir si ca converge.
Par exemple tend vers avec l la limite de

[legeniedesalpages]

ok, mais si je comprends bien on a pas besoin de parler des séries de référence de Riemann,
si on reprend tes arguments en effaçant les commentaires sur ces séries, c'est toujours bon, non?
je vois pas le rôle que joue ces séries de référence ici en fait. :hein:

[legeniedesalpages]

En modifiant un peu ton explication:

Les cas:

soit ne tend pas vers 0 et la serie de termes diverge et donc converge vers 0 car en - l'infini l'exponentielle tend vers 0.

soit tend vers 0 et alors cette suite est équivalente a et donc plusieurs cas suivant la manière dont tend vers 0.
Si la serie diverge alors le tout tend vers 0(idem qu'au 1). Soit la serie converge et le tout tend vers une limite fini avec l la limite de la serie .


Dans tout les cas ca converge.

Modifié comme ça c'est toujours bon?

[xunil]

Je dois dire une connerie, mais on voit facilement que (Un) est décroissante (le rapport Un / Un-1 = 1- xn < 1 ) et minorée par 0, donc elle converge. Non ?

[BQss]

Oui c'est bon, précise bien que la série est a terme positif, car diverger pour une série qui n'est pas de termes de signe constant ne signifie pas necessairement qu'elle tend vers l'infini et on ne pourrait conclure aussi aisément.
Ce que j'ai rajouté sur les series de références était juste une indication pour rendre plus claire la différence de cas, c'est un exemple et pas un élément de la réponse oui.

[BQss]

Je dois dire une connerie, mais on voit facilement que (Un) est décroissante (le rapport Un / Un-1 = 1- xn < 1 ) et minorée par 0, donc elle converge. Non ?

Ouai biensur mais suivant les cas ca tend vers 0 ou vers un réel de [0;1[.
Si non biensur, décroissante minorée, ca suffit pour dire que ca converge dans tout les cas mais le but c'est de voir comment suivant le comportement de .
Tu multiplies a chaque fois par un nombre positif inférieur à 1 donc oui ça décroit, biensur...

[legeniedesalpages]

BQss >> ok, à ce moment-là, j'ai compris. Oui effectivement c'est plus facile à visualiser avec les séries de Riemann.

xunil >> oui effectivement tu as raison, mais en fait j'avais besoin de plus de précision au niveau de son comportement.

En fait, je veux montrer que pour tout réel ,
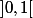
je peux trouver une suite de points de tel que l'ensemble de Cantor généralisé K associé à cette suite a pour mesure (de Lebesgue) .