Un entier
9 messages
- Page 1 sur 1
Si tu veux lire la réponse de notre aviateur : aviateurpilot
Personnellement j'y renonce les notations sont trop pénibles pour mon vieux cerveau
Imod
Personnellement j'y renonce les notations sont trop pénibles pour mon vieux cerveau
Imod
Imod a écrit:Si tu veux lire la réponse de notre aviateur : aviateurpilot
Personnellement j'y renonce les notations sont trop pénibles pour mon vieux cerveau
Imod
desolé, mais j'utlise bp les notations mathematqie a la place des mots, car je ne suis pas tres fort ni en englais ni en francais ,lol ,
mais surtout en englais, c'est pour cela que dans le site mathlinks, la pluspart des fois je ne conprend meme pas les probleme. et dans mes solutions je n'utilise que "so,then,if,=>,,<=" :ptdr:
Salut,
Je poste un peu en retard parce que j'étais en vacances^^. Après de longues recherches, voilà ce que j'ai:
Soit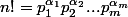
la décomposition en facteurs premiers de
Il s'agit de montrer que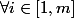
(a+2b)...(a+(n-1)b))
Soit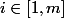
On écrit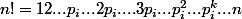
(je fais une démonstration descriptive, c'est plus facile en Latex^^)
A chaque fois que apparaît dans cette décomposition, on va lui associer un
apparaît dans cette décomposition, on va lui associer un  de
de (a+2b)...(a+(n-1)b)) de façon à montrer qu'on a bien
de façon à montrer qu'on a bien (a+2b)...(a+(n-1)b))
La première fois que apparaît, c'est pour
apparaît, c'est pour 
Si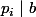 c'est bon.
c'est bon.
Sinon,
L'application
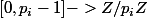
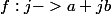
est injective donc bijective (ensemble de départ et d'arrivée finis de même cardinal)
Donc en particulier 0 est atteint et ainsi(a+2b)...(a+(n-1)b)) et apparaît dans sa décomposition.
et apparaît dans sa décomposition.
La deuxième fois que apparaît, c'est pour
apparaît, c'est pour 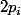
Cette fois-ci, on considère l'application
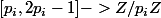
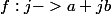
qui est pour les mêmes raisons que précédemment bijective. Ainsi, 0 est également atteint, et pour un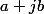 différent du précédent. Donc, dans le décompte, pour l'instant on a
différent du précédent. Donc, dans le décompte, pour l'instant on a 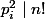 et
et (a+2b)...(a+(n-1)b)) : deux partout, c'est bon!
: deux partout, c'est bon!
On peut continuer de la même manière, jusqu'au premier "palier": lorsque la valuation p-adique double! Quand on arrive ainsi à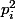 on considère d'abord comme d'habitude l'application
on considère d'abord comme d'habitude l'application
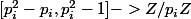
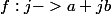
Arrivé à ce stade, il nous manque éventuellement une valuation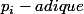 ; on la récupère en considérant
; on la récupère en considérant
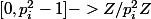
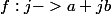
qui est encore bijective! Donc, le compte est bon.
Ainsi de suite, on montre que la valuation -adique de n! est plus petite que celle de
-adique de n! est plus petite que celle de (a+2b)...(a+(n-1)b)) ce qui nous permet de conclure!
ce qui nous permet de conclure!
Dites-moi si c'est faux ou si la rédaction est trop lacunaire!
Je poste un peu en retard parce que j'étais en vacances^^. Après de longues recherches, voilà ce que j'ai:
Soit
la décomposition en facteurs premiers de
Il s'agit de montrer que
Soit
On écrit
(je fais une démonstration descriptive, c'est plus facile en Latex^^)
A chaque fois que
La première fois que
Si
Sinon,
L'application
est injective donc bijective (ensemble de départ et d'arrivée finis de même cardinal)
Donc en particulier 0 est atteint et ainsi
La deuxième fois que
Cette fois-ci, on considère l'application
qui est pour les mêmes raisons que précédemment bijective. Ainsi, 0 est également atteint, et pour un
On peut continuer de la même manière, jusqu'au premier "palier": lorsque la valuation p-adique double! Quand on arrive ainsi à
Arrivé à ce stade, il nous manque éventuellement une valuation
qui est encore bijective! Donc, le compte est bon.
Ainsi de suite, on montre que la valuation
Dites-moi si c'est faux ou si la rédaction est trop lacunaire!
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
