salut, j'ai un probleme a resoudre qui coince
on veut mesurer la hauteur d'une tour construite sur un plateau.
pour cela on se place en un point B a gauche de cette tour qui voit le sommet sous un angle de 58°.
il n'est pas possible de mesurer la distance OB
on s'éloigne de 50 m supplementaire a gauche et du point A aligne avec O et B on voit le sommet sous un angle de 23°
quelle est la hauteur de la tour
Trigonometrie
7 messages
- Page 1 sur 1
Salut,
Disons que l'on appelle T le sommet de la tour. Et je crois deviner que l'on veut calculer OT.
Les triangles OTB et OTA sont rectangles en O. Du moins j'espère.
Avec les relations trigonométriques dans un triangle rectangle on a :
=\frac{OT}{OB}\text{ et }\tan(23^{\text{o}})=\frac{OT}{OA})
On peut en déduire :
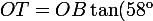=(OB+50)\tan(23^{\text{o}}))
La deuxième égalité permet de trouver OB, puis on calcule OT avec la première.
Disons que l'on appelle T le sommet de la tour. Et je crois deviner que l'on veut calculer OT.
Les triangles OTB et OTA sont rectangles en O. Du moins j'espère.
Avec les relations trigonométriques dans un triangle rectangle on a :
On peut en déduire :
La deuxième égalité permet de trouver OB, puis on calcule OT avec la première.
nuage a écrit:Salut,
Disons que l'on appelle T le sommet de la tour. Et je crois deviner que l'on veut calculer OT.
Les triangles OTB et OTA sont rectangles en O. Du moins j'espère.
Avec les relations trigonométriques dans un triangle rectangle on a :
On peut en déduire :
La deuxième égalité permet de trouver OB, puis on calcule OT avec la première.
MERCI EN FAIT C ETAIT SIMPLE POURQUOI CHERCHER COMPLIQUE
formules d' addition
bonjour
je suis en ce moment entr1 de bosser sur mon DM des vac. je pass en TS et je blok sur 1 kestion.
voici lénoncé de lexo:
ds le répére orthonormal direct ( o;i;j) on considére le point M de coordoné ( 2racinede3;2).
1) déterminer les coordoné polaires de M ds le repére (o:i)
> je lai fait et g trouver : (4; pi/6)
2) on considére le point N tel ke :
ON= 1/2OM et (OM;ON)= 3pi/4
> je trouve : (2;11pi/12) kom coordoné polaire.
3) en utilisan les formules d' addition , calculer: cos(11pi/12) et sin ( 11pi/12)
> VOILA POUVEZ VS MAIDER SUR LA KESTION 3 SVP!!!
je suis en ce moment entr1 de bosser sur mon DM des vac. je pass en TS et je blok sur 1 kestion.
voici lénoncé de lexo:
ds le répére orthonormal direct ( o;i;j) on considére le point M de coordoné ( 2racinede3;2).
1) déterminer les coordoné polaires de M ds le repére (o:i)
> je lai fait et g trouver : (4; pi/6)
2) on considére le point N tel ke :
ON= 1/2OM et (OM;ON)= 3pi/4
> je trouve : (2;11pi/12) kom coordoné polaire.
3) en utilisan les formules d' addition , calculer: cos(11pi/12) et sin ( 11pi/12)
> VOILA POUVEZ VS MAIDER SUR LA KESTION 3 SVP!!!
Salut,
Une petite piste si tu ne connais pas tes formules d'addition:
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+sinbcosa
sin(a-b)=sinacosb-sinbcosa
Maintenant essaie de voir si tu ne peux pas écrire 11pi/12 comme somme ou différence de 2 fractions ou valeurs bien connues...
ps: pense aussi à poster ton sujet autre part que dans celui d'un autre :marteau:
Une petite piste si tu ne connais pas tes formules d'addition:
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+sinbcosa
sin(a-b)=sinacosb-sinbcosa
Maintenant essaie de voir si tu ne peux pas écrire 11pi/12 comme somme ou différence de 2 fractions ou valeurs bien connues...
ps: pense aussi à poster ton sujet autre part que dans celui d'un autre :marteau:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 106 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
