Suites et sens de variation

par **titi** » 20 Aoû 2005, 14:10

Bonjour à tous !!!!! Savez-vous résoudre ce problème ???

Etudier le sens de variation des suites (Un), (Vn), et (Wn) définies sur N par :
Un= 2n+3/ n+4
Vn= n+5(-1)° °=exposant n
Wn= n²-2n+5

Merci de votre attention avec mes sincères salutations !!! :we: :we: :we:

par **Clain** » 20 Aoû 2005, 15:49

Pour étudier le sens de variation d'une suite (

), la méthode que j'utilise, et qui est utilisée communément je suppose, est d'étudier la différence entre

et

.

Ainsi, si on a avec n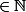

:

-

0
On sait que :

.

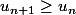Celà suffit pour dire que (

) est croissante.

Par exemple, pour (

) :

-

= (2(n+1) + 3) / ((n+1)+4) - (2n + 3) / (n+4)

par **Anonyme** » 20 Aoû 2005, 17:47

Tu peux faire, c'est assez rapide
Mais si tu veux t'éclater et que tu as un peu de temps devant toi, tu peux toujours t'amuser à assimiler les suites à des fonctions f(x),... , et te lancer dans une étude de fonction avec dérivation et tout le tralala.
J'ai lu une fois "Pourquoi faire simple quand on peut faire compliquer..........

par **titi** » 22 Aoû 2005, 11:50

N'y a t'il pas plusieurs autres maniières
:briques: :briques: :briques: NON ???????

par **Nightmare** » 22 Aoû 2005, 12:21

Bonjour

Tu peux aussi étudier le rapport U(n+1)/Un

:happy3:
Jord

par **Alpha** » 22 Aoû 2005, 12:43

D'accord, Jord,

mais on ne peut faire cela que si l'on sait que u est strictement positive. Si elle s'annule, ce rapport n'est pas tout le temps défini, et si elle change de signe, alors le rapport ne permet pas, à lui seul, de conclure.

Cordialement

par **Nightmare** » 22 Aoû 2005, 12:44

Non c'est sur alpha, mais aprés c'est à l'éléve de vérifier ces conditions.

par **titi** » 22 Aoû 2005, 19:06

merci beaucoup à tous

par **Clain** » 23 Aoû 2005, 00:26

"Triderou a écrit:Tu peux faire, c'est assez rapide
Mais si tu veux t'éclater et que tu as un peu de temps devant toi, tu peux toujours t'amuser à assimiler les suites à des fonctions f(x),... , et te lancer dans une étude de fonction avec dérivation et tout le tralala.

Par rapport à cette réponse, est-ce que ça se fait vraiment d'assimiler une suite à une fonction pour la dériver et trouver son sens de variation ?
Si mes souvenirs sont exacts, la suite est bien comme une fonction mais définie sur

, peut-on alors la dériver sur

?
La technique me semble plus simple qu'avec les

et

(Les dérivées, je commence à maîtriser.) mais les justifications de la méthode quelque peu sombres.

J'avoue que cette année, avec mon prof, on a toujours utilisé la différence des termes successifs, parfois le rapport, quand l'occasion s'y prêtait, et que je n'ai jamais pensé à une autre méthode.

Question triviale, il est vrai, mais à laquelle je trouve intérêt.

par **Nightmare** » 23 Aoû 2005, 00:53

Bonjour :happy3:

Il faut savoir que si une fonction est croissante(resp. décroissante) sur un ensemble E, alors elle est croissante(resp. décroissante) sur tout sous-ensemble de E.
Donc si l'on arrive à prouver par exemple q'une fonction f est croissante sur R+, alors elle sera a fortiori croissante sur N, donc la suite Un=f(n) est croissante.

Donc si l'on donne une suite Un=f(n) et qu'on prouve que f est monotone sur un intervalle [a,b], alors (Un) est de même monotonie sur l'intervalle [|a;b|] (c'est à dire l'intervalle [a,b] restreint à ses éléments entiers)

C'est comme cela que marche le raisonnement

:happy3:
Jord

par **Clain** » 23 Aoû 2005, 01:10

Tout simplement ! Merci bien.

Sinon, pendant que je te tiens, t'aurais pas une explication soft sur la question de l'infinité de points de l'autre topic ? Mathador l'a locké avant que j'aie le temps de demander ça.
Par soft j'entends sans matrice carrée (parce que je n'en ai aucune définition) et sans "n=p=rg(A)" aussi parce que je sais pas ce que ça signifie. :D (Cela dit, si tu te sens de m'entretenir sur cela aussi, je prends hein ; )

Edit : Et mathador qui n'est pas là, étrange ces gens qui dorment pendant la nuit ! Bon, j'attendrai un peu alors. : )

par **Nightmare** » 23 Aoû 2005, 01:31

Il faudrait que mathador réouvre le topic car je ne vais pas "polluer" celui de titi par des explications sur les matrices ...

par **Alpha** » 23 Aoû 2005, 08:03

Bonjour à vous,

Si Clain a des questions à poser à Jord sur un sujet précis et différent de cette discussion-là, il peut très bien ouvrir un nouveau topic sur cela.

par **Nightmare** » 24 Aoû 2005, 00:40

Le probléme alpha est que les questions que veut me poser Clain sont en rapport avec une discussion fermé par Mathador (Je pense qu'il l'a fermé parcequ'il devait être jaloux

je rigole bien sur). Est-ce que cela vaut le coup d'ouvrir un autre topic où pouvez vous juste réouvrire l'autre ?

:happy3:
Jord

par **Alpha** » 24 Aoû 2005, 08:15

Salut, Nightmare!

Ca dépend... Avez-vous vraiment besoin de l'autre topic pour poursuivre? De toute façon, vous avez accès à ce qui a déjà été écrit... Le problème, c'est que si l'on ouvre un topic, qu'on commence à parler de quelque chose, puis que ça détive sur autre chose, puis qu'on continue sur ce topic parce que c'est plus pratique, puis que ça dérive sur encore autre chose... On s'en sort plus, quoi.

Avant de prendre toute décision, j'en parlerai avec Mathador, dès que je lui parlerai :happy:. Mais peut-être aura-t-il pris une décision avant que je puisse lui parler.

Amicalement

par **titi** » 24 Aoû 2005, 08:49

bonjour j'ai un problème ,un vrai,lol, j'ai trouvé Un et Wn mais j'ai vraiment du mal pour Vn quelqu'un peut m'aider ?????

par **julian** » 24 Aoû 2005, 10:54

Ta suite

c'est bien

?

par **Nightmare** » 24 Aoû 2005, 11:13

Moi je n'en sais rien alpha, ce n'est pas pour moi que je dis ça mais pour clain.

titi, tout dabord, fait des conjecture sur le sens de variation, ça t'aidera pour faire la démonstration

Ensuite utilise le fait que si n est pair, (-1)^n=1 et si n est impair (-1)^n=-1

:happy3:
Jord

Suites et sens de variation

Suites et sens de variation

....Et je dirais même plus.......

Question triviale

Qui est en ligne