Arithmetique
Olympiades mathématiques, énigmes et défis
-
altusi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Aoû 2005, 21:06
-
 par altusi » 22 Aoû 2005, 21:39
par altusi » 22 Aoû 2005, 21:39
prouver que pour tout naturel n>0 il existe un naturel k>0 tel que 2^nk admet une representation decimale ne contenant que les chiffres 1 et 2
(pas vraiment dur...)
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 25 Aoû 2005, 23:14
par Chimerade » 25 Aoû 2005, 23:14
altusi a écrit:prouver que pour tout naturel n>0 il existe un naturel k>0 tel que 2^nk admet une representation decimale ne contenant que les chiffres 1 et 2
(pas vraiment dur...)
Ta notation est ambiguë. Tu veux dire

ou

-
altusi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Aoû 2005, 21:06
-
 par altusi » 26 Aoû 2005, 07:26
par altusi » 26 Aoû 2005, 07:26
Ah oui,c'est vrai, :marteau:
c'est plutot (2^n) multiplie par k :zen:
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 26 Aoû 2005, 10:54
par Chimerade » 26 Aoû 2005, 10:54
altusi a écrit:prouver que pour tout naturel n>0 il existe un naturel k>0 tel que 2^nk admet une representation decimale ne contenant que les chiffres 1 et 2
(pas vraiment dur...)

par exemple :

, soit 1 avec n "zéros". Pas mal le coup du 2 : c'était pour tromper l'ennemi ?
-
phenomene
- Membre Relatif
- Messages: 313
- Enregistré le: 04 Aoû 2005, 07:09
-
 par phenomene » 26 Aoû 2005, 11:04
par phenomene » 26 Aoû 2005, 11:04
Chimerade a écrit:
par exemple :

, soit 1 avec n "zéros". Pas mal le coup du 2 : c'était pour tromper l'ennemi ?
Il me semble que

est un chiffre distinct de

et

...
-
Chimerade
- Membre Irrationnel
- Messages: 1472
- Enregistré le: 04 Juil 2005, 13:56
-
 par Chimerade » 26 Aoû 2005, 11:16
par Chimerade » 26 Aoû 2005, 11:16
phenomene a écrit:Il me semble que

est un chiffre distinct de

et

...
OOOPS ! Tu as raison, merci de le remarquer ! Ca m'apprendra à lire !
Désolé Altusi, au temps pour moi, je n'ai rien dit :pc:
-
Galt
- Membre Rationnel
- Messages: 789
- Enregistré le: 13 Aoû 2005, 12:03
-
 par Galt » 26 Aoû 2005, 11:24
par Galt » 26 Aoû 2005, 11:24
C'est amusant, je ne connaissais pas.
Remarque :dans cete énigme, on peut remplacer 1 et 2 par n'importe quel couple de chiffres, s'il y en a un pair et un impair.
Je laisse chercher le forum.
-
Anonyme
 par Anonyme » 17 Sep 2005, 19:47
par Anonyme » 17 Sep 2005, 19:47
Chimerade a écrit:Ta notation est ambiguë. Tu veux dire

ou

c vraiment difficile mais chwi encore en vacance" moi
-
altusi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Aoû 2005, 21:06
-
 par altusi » 17 Sep 2005, 21:25
par altusi » 17 Sep 2005, 21:25
on pourra utiliser la recurrence par exemple!
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 17 Juin 2006, 17:19
par aviateurpilot » 17 Juin 2006, 17:19
on pose

avec

admet une representation decimale ne contenant que les chiffres 1 et 2
=> si
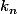
est pair alors on pose
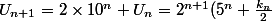)
=> si
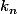
est impair alors on pose
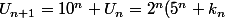=2^{n+1}(\frac{5^n+k_n}{2}))
dans les deux cas

divisible par
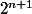
donc il existe
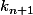
tel que
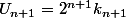
et en plus

a une representation decimale ne contenant que les chiffres 1 et 2
donc s'il existe
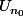
qui verifie qui admet une representation decimale ne contenant que les chiffres 1 et 2 et qui est divisible par
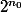
alors quelque soit n>ou=


verifie les conditions
or on a 1 et 2 verifie ces conditions donc pour tout naturel n>0 il existe un naturel k>0 tel que
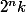
admet une representation decimale ne contenant que les chiffres 1 et 2
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 17 Juin 2006, 21:14
par yos » 17 Juin 2006, 21:14
L'exposant du 10 n'a aucune raison d'être n à mon avis. Il faut un exposant
f(n) par exemple
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 17 Juin 2006, 22:42
par aviateurpilot » 17 Juin 2006, 22:42
il existe un naturel k>0
on veux seulement montrer l'existance
moi j'ai fait un exemple
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 18 Juin 2006, 11:28
par yos » 18 Juin 2006, 11:28
J'ai bien compris mais tes Un ne conviennent pas tels qu'ils sont construits. Il faut que

soit fabriqué en tenant compte du nombre de chiffres de Un .

, dans le cas où kn est impair par exemple.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Juin 2006, 12:52
par aviateurpilot » 18 Juin 2006, 12:52
on prend par exemple
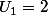
dans ce cas
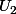
va etre construi pas 2 chiffres
et
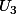
de 3 chiffres
...
..
....et

de n chiffres
alors si on ajoute
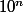
ou

c comme si on ajoute 1 ou 2 à gauche de la representation de

(dans la base 10)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 18 Juin 2006, 13:02
par yos » 18 Juin 2006, 13:02
Oui c'est bon. J'avais lu un peu vite. Elle est bien ta suite.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 18 Juin 2006, 13:09
par aviateurpilot » 18 Juin 2006, 13:09
ok yos :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
ou
 avec
avec  admet une representation decimale ne contenant que les chiffres 1 et 2
admet une representation decimale ne contenant que les chiffres 1 et 2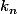 est pair alors on pose
est pair alors on pose 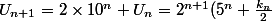)
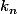 est impair alors on pose
est impair alors on pose 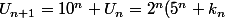=2^{n+1}(\frac{5^n+k_n}{2}))
 divisible par
divisible par 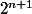 donc il existe
donc il existe 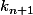 tel que
tel que 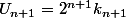 et en plus
et en plus  a une representation decimale ne contenant que les chiffres 1 et 2
a une representation decimale ne contenant que les chiffres 1 et 2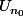 qui verifie qui admet une representation decimale ne contenant que les chiffres 1 et 2 et qui est divisible par
qui verifie qui admet une representation decimale ne contenant que les chiffres 1 et 2 et qui est divisible par 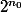 alors quelque soit n>ou=
alors quelque soit n>ou= 
 verifie les conditions
verifie les conditions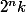 admet une representation decimale ne contenant que les chiffres 1 et 2
admet une representation decimale ne contenant que les chiffres 1 et 2