Dénombrement

par **Elise77** » 10 Juil 2007, 16:15

Bonjour à tous,

Voilà, je révise pour un concours et je bloque comme je m'en doutais au niveau des probas et au tout début sur le dénombrement.

J'ai un petit exercice (le premier en fait...) qui me laisse perplexe. Je pense que je n'arrive pas à bien comprendre l'énoncé, du coup, je me trompe dans la résolution.

Voici mon problème:

" Une PME compte 14 employés, qui chaque matin se serrent la main. Combien y'a t-il de poignées de main échangées chaque matin?"

Pour moi, un employé sert la main à 13 autres puis le 2 à 12 etc.. jusqu'à avoir au final 13 factoriel poignées de main.

Mais la correction fait appel à une combinaison avec p=2 et n=14.

Pour mon interprétation, je compte une poignée de main entre deux employés et dans la correction, elle semble compter pour deux et ca, je ne le comprends pas.

Pourriez-vous m'éclairer? Ou me dire pourquoi je me trompe?

merci d'avance pour votre aide.

par **bigzpanda** » 10 Juil 2007, 16:19

Le problème expliqué sur:
http://perso.orange.fr/therese.eveilleau/pages/truc_mat/textes/escalier.htm
Section Applications
Penses tu vraiment que 6227020800 (13!) poignées de mains c'est possible :p ?

par **Cyberlilu** » 10 Juil 2007, 16:25

Elise77 a écrit:un employé sert la main à 13 autres puis le 2 à 12 etc.. jusqu'à avoir au final 13 factoriel poignées de main.

réfléchis bien à ce que tu dis!! logiquement toutes les personnes sert la main à un même nombre de personne!!

par **emdro** » 10 Juil 2007, 16:27

Elise77 a écrit:
Pour moi, un employé sert la main à 13 autres puis le 2 à 12 etc.. jusqu'à avoir au final 13 factoriel poignées de main.

Tu n'es pas loin, mais tu fais à la fin 13*12*11... Mais pourquoi ces multuplications? Il faut additionner: 13+12+11+...+1
Donc cela te donne 14*13/2 (somme des n premiers nombres).

Une façon de voir ce problème est de faire un tableau à double entrée avec les 14 employés d'un côté (vertical) et les 14 employés (horizontal).
On ne se serre pas la main à soi-même, donc tu ôtes la diagonale. (il reste 14²-14 cases). Et si A serra la main à B ou B serre la main à A, c'est pareil. Donc tu peux ôter la moitié des cases (au-dessus ou en dessous de la diagonale). Cela donne (14²-14)/2 poignées de main.

L'histoire des combinaisons, c'est encore un autre raisonnement: une poignée de main, c'est un choix de 2 personnes parmi 14. Il y a bien sur (2 parmi 14) tels choix.

par **Elise77** » 10 Juil 2007, 16:29

oh merci beaucoup, évidemment que 13 factoriel c'était douteux mais j'avoue que je ne comprenais pas bien le truc.

J'ai bien compris la correction qui me parait très logique en effet, mais comment relie-t-on: (14*13)/2 donc ((n-1)(n))/2 à la combinaison?

Je crois que je ne comprends pas comment déterminer le p dans ce cas là.

Edition du message: merci pour vos réponses. Je vais tacher de me concentrer un peu sur p

par **emdro** » 10 Juil 2007, 16:39

Eh bien, c'est simplement la formule:

,
cas particulier de

(ancienne notation du coefficient binomial)

C'est le raisonnement 14 choix pour la première personne. Pour chacun de ces choix (donc * et non+ cette fois!), 13 choix pour la deuxième. Et comme l'ordre ne compte pas, on divise par 2.

par **Elise77** » 10 Juil 2007, 16:48

ok merci, je n'avais pas la formule simplifiée pour p=2

Euh...j'ai un autre problème. Et oui!

Finale du 100 m, 8 candidats et un podium de 3 places. On demande le nombre de podium différents à l'arrivée.

perso je me suis dit que ca pouvait être modélisé comme un tirage de trois boules simultanées sur 8 avec remises à chaque fois. Ce qui me faisait prendre la combinaison. je trouvais donc 56 podiums possibles.

La correction donne 8*7*6=336.

je comprend bien la réponse donnée, mais je ne vois pas ce qui, dans l'énoncé, peux faire penser à ca...

En fait, je me trompe à chaque fois, pour un probleme de lecture de l'énoncé.
Y'at-il un petit truc qui pourrait m'aider?

par **emdro** » 10 Juil 2007, 16:54

Elise77 a écrit:Finale du 100 m, 8 candidats et un podium de 3 places. On demande le nombre de podium différents à l'arrivée.

perso je me suis dit que ca pouvait être modélisé comme un tirage de trois boules simultanées sur 8 avec remises à chaque fois. Ce qui me faisait prendre la combinaison. je trouvais donc 56 podiums possibles.

Avec remise? Tu peux avoir la même personne pour l'or et pour l'argent?
Combinaisonordre indifférent: donc, c'est une mauvaise idée les combinaisons ici.

Réfléchis simplement et concrétement: tu te mets à l'arrivée et tu attends: Le premier arrive (8 choix) puis le deuxième (7 choix) et enfin le troisième (6 choix). Bilan 8*7*6 arrivées possibles.

par **Elise77** » 10 Juil 2007, 16:58

mais si on tire trois candidats sur les 8 une fois et qu"on les remet ensuite, on a pas deux candidats pour la meme place? on aura trois autres.

je crois vraiment qu"il y a là une subtilité que je ne pige pas. Je crois qu'à choisir, je prefere les suites!

par **Elise77** » 10 Juil 2007, 17:06

ca y est, pour ce coup mà je crois que j'ai compris, merci encore de votre patience

par **emdro** » 10 Juil 2007, 17:07

Elise,

pour t'aider, dans un tirage de p boules parmi n tu dois distinguer

*Avec remise + L'ordre compte
Le résultat est décrit par une liste de p éléments choisis parmi n.
n choix pour le premier, n pour le deuxième...

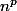choix possibles

*Sans remise + L'ordre compte
Le résultat est décrit par une liste de p éléments distincts choisis parmi n.
n choix pour le premier, n-1 pour le deuxième...

choix possibles. C'est

*L'ordre ne compte pas
Le résultat est décrit par un sous-ensemble de p éléments distincts choisis parmi n.
n choix pour le premier, n-1 pour le deuxième..., mais on divise à la fin par p!, le nombre de permutations de ces p éléments

choix possibles. C'est

Donc les questions importantes sont:
tirages successifs (2 premiers cas) ou simultanés (le dernier)?
avec ou sans ordre?

NB lors de tirages simultanés, l'ordre ne peut intervenir puisqu'on prend toutes les boules en même temps.

par **emdro** » 10 Juil 2007, 17:14

Efforce-toi, dans chaque exo de dénombrement, de te demander comment tu vas décrire un des résultats choisis par le hasard.

Par exemple, pour la course:
Une liste (avec ordre), un ensemble (pas d'ordre)?
---> une liste, l'or en premier, l'argent en 2...
Avec remise, sans remise?
--->sans remise (tu ne veux pas le même nom deux fois);

Voilà!

par **kz junior 11!** » 19 Mar 2012, 15:45

Elise77 a écrit:Bonjour à tous,

Voilà, je révise pour un concours et je bloque comme je m'en doutais au niveau des probas et au tout début sur le dénombrement.

J'ai un petit exercice (le premier en fait...) qui me laisse perplexe. Je pense que je n'arrive pas à bien comprendre l'énoncé, du coup, je me trompe dans la résolution.

Voici mon problème:

" Une PME compte 14 employés, qui chaque matin se serrent la main. Combien y'a t-il de poignées de main échangées chaque matin?"

Pour moi, un employé sert la main à 13 autres puis le 2 à 12 etc.. jusqu'à avoir au final 13 factoriel poignées de main.

Mais la correction fait appel à une combinaison avec p=2 et n=14.

Pour mon interprétation, je compte une poignée de main entre deux employés et dans la correction, elle semble compter pour deux et ca, je ne le comprends pas.

Pourriez-vous m'éclairer? Ou me dire pourquoi je me trompe?

merci d'avance pour votre aide.

tu sais les 14 employer du PME sont non ordonné en se serrant la main et sont 2 à 2 distincts c'est donc une combinaison
la formule c'est C,n,p=n!/p!(n-p)!.
:we:
pour le résultat:

soit E l'ensemble des employer du PME
E=14
une poignée de main est une famille de 2 élément de E deux à deux distinct non ordonné c'est donc une combinaison
C;14;2 =14!/2!(14-2)!
=14x13x12!/2!x12! on simplifie 12!
=14x13/2 on simplifie par 2
=7x13
=91 poignées de main

Dénombrement

Dénombrement

Qui est en ligne