Fonctions équivalentes

[pierrem]

Bonjour
J'ai une question sur les fonctions équivalentes en + infini. On considère f dérivable.

Si f ~ x^2 a-t-on f'(x)~2x ? Etudier la réciproque.

J'ai vu en cours le contre-exemple f(x)= x^2+xsin x mais pour la réciproque je ne vois pas de contre exemple...

Merci par l'aide

[Ledescat]

Je ne sais plus comment le montrer, mais tu as toujours le droit d'intégrer un DL, mais pas de le dériver à coup sûr.

[quinto]

Je ne sais plus comment le montrer, mais tu as toujours le droit d'intégrer un DL, mais pas de le dériver à coup sûr.

Oui enfin ici il ne s'agit pas de dl mais d'équivalent, ce qui est sensiblement différent.

[Ledescat]

C'était une idée comme ça!

[pierrem]

C'était une idée comme ça!

En fait je viens de rétrouver une règle de l'Hospital. Puisque lim(f '(x)/2x)=1 alors lim(f(x)/x^2 )=1.

[Lierre Aeripz]

Ce théorème se résout en une ligne à l'aide du théorème de sommation des relations de comparaison.

En voici une partie :
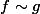
Soit , tel que et f ne soit pas intégrable.
Alors .

(J'aimerais bien écrire "équivalent quand x tend vers l'infini" mais je ne sais pas comment mettre le sous le ...)

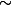
[Lierre Aeripz]

En fait je viens de rétrouver une règle de l'Hospital. Puisque lim(f '(x)/2x)=1 alors lim(f(x)/x^2 )=1.

Oui, cela marche aussi. A condition d'utiliser la généralisation de la généralisation de cette règle...
En toute honnêteté, cette règle est un bricolage qui ne sert jamais. Il existe des outils (comme le théorème que je t'ai donné) bien plus généraux et bien plus naturels.

[B_J]

[B_J]

(J'aimerais bien écrire "équivalent quand x tend vers l'infini" mais je ne sais pas comment mettre le sous le ...)

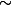
ou

[B_J]

ou

ou

etc