Inégalité!!
Olympiades mathématiques, énigmes et défis
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 28 Juin 2007, 18:15
par Mohamed » 28 Juin 2007, 18:15
coucou les amis, en retour sur le forum des olympiades ...
soit a,b,c >0 tel que
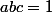
Mq

BNE CHANCE
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 28 Juin 2007, 18:35
par Imod » 28 Juin 2007, 18:35
Bonjour .
Il suffit de montrer que

. Il me semble avoir vu ça il y a peu .
Imod
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
 par Mohamed » 28 Juin 2007, 22:30
par Mohamed » 28 Juin 2007, 22:30
il faut rédiger Imod, pas parler comme ça....!!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 28 Juin 2007, 22:49
par Joker62 » 28 Juin 2007, 22:49
Ben y'a rien à rédiger
On a
ab = 1/c
bc = 1/a
ac = 1/b
On réduit tout
On revient à
1/c + 1/a + 1/b >= 3
Voilà reste juste ça à démontrer.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 29 Juin 2007, 08:38
par Imod » 29 Juin 2007, 08:38
En fait c'est l'inégalité des moyennes arithmétiques et géométriques :

avec
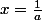
,
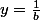
,
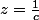
.
Imod
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 29 Juin 2007, 10:00
par Sylar » 29 Juin 2007, 10:00
Bonjour ,conscience c'est mieux.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Juin 2007, 12:58
par lapras » 30 Juin 2007, 12:58
salut,
interessante cette inégalité, aurais tu la démonstration ?
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 30 Juin 2007, 16:22
par Imod » 30 Juin 2007, 16:22
Je suppose que tu parles de ça :
C'est une des nombreuses inégalités de convexité ( à bien connaître quand on s'attaque aux inégalités de type olympiade ) . Celle-ci se démontre facilement en utilisant la concavité de ln(x) sur
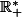
:
\geq ln(\frac{x}{3}+\frac{y}{3}+\frac{z}{3})\geq\frac{ln(x)}{3}+\frac{ln(y)}{3}+\frac{ln(z)}{3}\geq \frac{ln(xyz)}{3}})
etc ...
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Juil 2007, 10:49
par lapras » 01 Juil 2007, 10:49
je connais que le log(x), le ln c'est la dérivée de log ??
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Juil 2007, 11:20
par Imod » 01 Juil 2007, 11:20
lapras a écrit:je connais que le log(x), le ln c'est la dérivée de log ??
Je ne suis pas très au courant des notations actuelles ! Pour moi :
ln : logarithme néperien
log : logarithme décimal
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Juil 2007, 11:30
par lapras » 01 Juil 2007, 11:30
Ok c'est pareil pour moi, mais je n'ai que vu rapidement le log. je ne connais que de nom le logarithme népérien.
-
~oa~
- Membre Naturel
- Messages: 40
- Enregistré le: 02 Juil 2007, 18:38
-
 par ~oa~ » 02 Juil 2007, 19:07
par ~oa~ » 02 Juil 2007, 19:07
salut
puisqu'on a
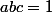
alors on peut poser :
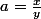
et:
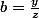
et :
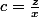
on a



et d'aprés MG_AM on a:

^( \frac{1}{3}))
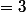
d'où:

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités