Racines complexes

[restonsmodeste]

Bonjour,

Cela fait 2 jours que je bute sur l'équation suivante:

i z^2+(4i-3)z + i - 5 ) = 0

j'ai fais la méthode algébrique (séparation partie réelle et imaginaire et résolution par système) mais j'ai beau substituer et faire des combinaisons linéaire je n'aboutie pas... Si vous pouviez détailler l'étape du système.

merci d'avance pour le coup de main.

[bigzpanda]

Salut,
Voilà comment faire:
Utilise la formule de résolution des équations du deuxième degré:

Calcule les racines de delta, avec Moivre ou en faisant un système. Tu trouveras deux racines, d1 et d2 qui appartienent à C.
Ensuite, utilise:

Tu vas donc trouver deux z qui appartiennent à C, tes deux solutions
Reste ensuite à les mettre sous la forme a+bi.

Si tu as de la peine, n'hésite pas à demander des précisions...

[emdro]

i z^2+(4i-3)z + i - 5 = 0

Bonjour,

tu poses z=x+iy et donc tu as z²=(x²-y²)+i(2xy)

i z^2+(4i-3)z + i-5 = 0
i[(x²-y²)+i(2xy)] +(4i-3)(x+iy)+ i-5 = 0
[-2xy-3x-4y-5]+i[x²-y²+4x-3y+1] = 0
[-2xy-3x-4y-5]=0 et [x²-y²+4x-3y+1] = 0

De la première équation, tu tires

La deuxième s'écrit


D'où


En posant

tu obtiens

Donc (discriminant...)
X=1 ou

Comme
C'est nécessairement
Donc x=-1 [et donc y=-1] ou x=-3 [et donc y=-2].

Voilà! Deux solutions: -1-i et -3-2i

[emdro]

Utilise la formule de résolution des équations du deuxième degré:

Calcule les racines de delta

En TS, les formules sont au programme uniquement pour a,b et c réels. Donc, cette méthode est inenvisageable.

[bigzpanda]

Pourtant rien ne change dans la démonstration, que les coéfficient soient réels ou complexes.(c.f. ici par exemple )

Je trouve également -1-i et -3-2i....et c'est beaucoup plus rapide !

[emdro]

Rien de change, sauf qu'à un moment, il faut trouver les racines carrées d'un nombre complexe (alors qu'il est réel si a,b,c sont réels). Et cela n'est pas au programme.

D'ailleurs tu commets toi même une erreur en notant alors que ton n'est pas un Réel Positif, mais un nombre complexe. Cette notation n'est pas admise.

[bruce.ml]

Pas d'accord ! La notation mentionne UNE racine nième de z. Je trouve ça très hypocrite de la part de certains matheux de raler sur une racine nième complexe, et d'autoriser derrière un , alors que , et qu'on a parfois ( SOUVENT ) besoin de considérer les deux racines carrées de 4 !

[quinto]

Pas d'accord ! La notation mentionne UNE racine nième de z. Je trouve ça très hypocrite de la part de certains matheux de raler sur une racine nième complexe, et d'autoriser derrière un , alors que , et qu'on a parfois ( SOUVENT ) besoin de considérer les deux racines carrées de 4 !

Je suis entièrement d'accord avec ça.
On nous fatigue pendant des années de lycée et de prépa à nous dire que ça n'a pas de sens et dès que l'on commence à faire de l'analyse complexe, on se rend compte, non seulement que ça a du sens, mais que tout le monde l'écrit.
On trouve même très souvent, de la part des algébristes ce que j'aime un peu moins cependant.

A la limite que l'on interdise la notation au lycée, je suis d'accord. Pour le reste, je trouve ça inutile.

[quinto]

Evidemment, ces remarques ne sont pas personnellement adressées à emdro :)

[emdro]

autoriser derrière un , alors que , et qu'on a parfois ( SOUVENT ) besoin de considérer les deux racines carrées de 4 !

Donc un raisonnement du genre
x²=4 x=
ne vous gênerait pas, puisque la prend en compte les deux racines carrées de 4? Les deux en même temps, ou l'une des deux au choix? Dans ce cas c'est le sens de qui est à revoir?

Bon, vous écrivez ça dans votre coin, d'accord. A la limite, vous le faites avec un public averti, d'accord.
Maintenant, si vous vous amusez à balancer de genre d'écriture à des élèves qui n'ont pas votre recul mathématique, on va à la catastrophe. Et cela n'a rien à voir avec la prétendue hypocrisie que vous dénoncez.

En l'occurence, croyez vous que "Restonsmodeste" qui pose cette question ait un énorme background d'analyse complexe? De quoi a-t-il besoin comme réponse quand il pose cette question?

Quel est l'intérêt de donner une telle équation à résoudre? Regardez un peu le contenu mathématique de la méthode que j'ai proposée. Ce ne serait pas un peu plus intéressant que d'appliquer une formule bêtement?

Il m'avait semblé que se poser la question était trouver la réponse.

[quinto]

En l'occurence, croyez vous que "Restonsmodeste" qui pose cette question ait un énorme background d'analyse complexe? De quoi a-t-il besoin comme réponse quand il pose cette question?

Non c'est pour cela que je disais qu'en terminale, je trouvais raisonnable de proscrire cette notation

a+

[bigzpanda]

Ce ne serait pas un peu plus intéressant que d'appliquer une formule bêtement?

Quelle formule à applquer bêtement ?
Pour trouver les racines il suffit d'utiliser Moivre(qui se démontre sans dificulté), ou même simplement un système si Moivre n'est pas au programme !

Et pour si c'est pour la formule du deuxième degré, la démonstration est facile et faite en cours(je crois programme de 1ère...)

[bruce.ml]

Non je ne parlais pas de ce dont tu parles dans ton exemple. Ce qui me dérange c'est qu'on ne veuille pas écrire 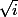mais qu'on écrive dans le même contexte des nombres complêxes 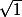. Là on se paume TRES rapidement.

Sinon sur l'utilisation des radicaux dans les complêxes, je n'ai pas vraiment d'avis. Je les utilise car j'en ai l'habitude, mais il faut faire attention quand on est novice, c'est comme avec les notation de Landeau.

[restonsmodeste]

Merci pour la résolution de l'équation et pour vos interventions instructives.