équation dans C
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 27 Juin 2007, 22:50
par axiome » 27 Juin 2007, 22:50
Bonjour,
Voilà, avec les vacances qui sont là, j'ai voulu m'y remettre un peu pour le fun, et j'ai malheureusement perdu le corrigé de cet exercice. Pourriez-vous m'aider ?
Résoudre dans C :
z^4 + z^3 + z^2 + z + 1 = 0
Bon, je sais que la première chose à faire est de vérifier que 0 n'est pas racine de ce polynôme afin de pouvoir factoriser par z^2 et ensuite simplifier ce polynôme par z^2. On obtiendrait, comme 0 n'est pas racine :
z^2 + z + 1 + (1/z) + (1/z^2) = 0
Ensuite je crois qu'il faut poser u= qqch. Mais là, trou noir.
Merci d'avance de vos réponses.
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Juin 2007, 22:55
par Sylar » 27 Juin 2007, 22:55
bONSOIR ,je vois pas trop l'utilité de factoriser par z^2....
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 27 Juin 2007, 23:21
par muse » 27 Juin 2007, 23:21
a mon avi c'est plutot le contraire si c'est 0 qui est solution alors on factorise par z et on simplifie par z et on reregarde si 0 est solution jusqu'a ce que se 0 ce soit plus solution et on resoud par des choses conue si c'est du second degres aors delta etc.. si c'est du troisieme degres on cherche une solution évidente et pareille pour degres 4 5 6 7 ...
La en l'ocurrence je ne vois pas trop ...
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 27 Juin 2007, 23:27
par muse » 27 Juin 2007, 23:27
en meme temps on fait pas ça au lycée je ne sais pas ou tu as vu sa ....
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Juin 2007, 23:30
par Sylar » 27 Juin 2007, 23:30
Exact ca me parait pas si simple ,pas du niveau lycée.
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 27 Juin 2007, 23:34
par muse » 27 Juin 2007, 23:34
j'ai cherché une solution evident j'ai pas trouvé enfin j'ai pas bcp chercher ...
faut vérifier sur maple les solutions je regarderai ce soir sur un autre PC c'est quoi les solution et si y'a une solution evidente je vous le dirai :p
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Juin 2007, 23:35
par Sylar » 27 Juin 2007, 23:35
Ok merci...
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 27 Juin 2007, 23:53
par Sylar » 27 Juin 2007, 23:53
Ah bien joué Rain ;les racines 5 ieme de l'unité.... :we:
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 28 Juin 2007, 00:16
par muse » 28 Juin 2007, 00:16
je ne connaissais pas cette technique en fait que tu as :
z^n+....z²+z+1=0
il faut calculer
(z-1)(z^n+....z²+z+1)=z^(n+1)-1
ensuite c'est facile ...
Je ne suispas sur que axiome sache resoudre: z^n=1 aussi enfin c'est pasc compliqué sa :)
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 28 Juin 2007, 03:36
par allomomo » 28 Juin 2007, 03:36
Salut,
Un coup d'oeil [url="http://rifly01.free.fr/docs/maths/exercices/37.pdf?cle=96&%20id="]là[/url] (
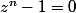
...)
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 28 Juin 2007, 09:22
par emdro » 28 Juin 2007, 09:22
axiome a écrit:z^2 + z + 1 + (1/z) + (1/z^2) = 0
Ensuite je crois qu'il faut poser u= qqch.
Bonjour,
oui pour ce genre d'équations polynomiales symétriques, on pose en général
u=z+1/z (lorsque 0 n'est pas une racine).
u²=z²+1/z²+2
Du coup, ton équation est équivalente à u²+u-1=0 (sauf erreur).
Tu trouves u et ensuite, en résolvant à nouveau deux équations du second degré, tu trouves les 4 solutions.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 28 Juin 2007, 09:31
par axiome » 28 Juin 2007, 09:31
Oui emdro, merci, je crois que c'est ça. Je vais essayer.
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 28 Juin 2007, 10:19
par emdro » 28 Juin 2007, 10:19
@Rain',
Non, ce n'est pas au programme de TS.
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 28 Juin 2007, 10:30
par emdro » 28 Juin 2007, 10:30
Si, vous faisiez du hors programme: flagrant délit sur ce coup-là!
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 28 Juin 2007, 12:45
par Nicolas_75 » 28 Juin 2007, 12:45
Bonjour,
Si on a "oublié" que z^5 -1 = (z-1)(z^4+z^3+z^2+z+1), il suffit d'observer que z^4+z^3+z^2+z+1 est la somme des termes d'une suite géométrique de raison z.
Cordialement,
Nicolas
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 29 Juin 2007, 00:30
par muse » 29 Juin 2007, 00:30
Rain' a écrit:Y a un problème dans la correction 2, et si z= 1 ?
Alors 1 est solution de (z-1)(z^4+z^3+z^2+z+1), pas tres etonnant mais ce qui nous interesse c'est les autre solutions ...
C'est pareille que une suite geometrique ...c'est exactement la meme formule.
z^4+z^3+z^2+z+1=(z^5-1)/(z-1)
-
kiwis939
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Juin 2007, 12:45
-
 par kiwis939 » 29 Juin 2007, 12:50
par kiwis939 » 29 Juin 2007, 12:50
-
kiwis939
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Juin 2007, 12:45
-
 par kiwis939 » 29 Juin 2007, 12:51
par kiwis939 » 29 Juin 2007, 12:51
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
