Corps engendré par une partie !

[nuage]

Salut,

[...]

P.S : Yos, je vois pas comment faire pour montrer qu'il n'y'a pas de corps strictement entre et :mur: !!!

C est une extension de degré 2 sur R. Et il n'y a pas d'entier entre 1 et 2.

[barbu23]

Yos, on peut voir comme un sous-espace vectoriel de dimension 1 de l'espace vectoriel qui est de dimension 2, et si on suppose qu'il existe un sous corps strictement entre et qu'on notera par exemple alors c'est à dire et ( absurde ) .

[barbu23]

oui voilà merçi Sarmate et nuage !!

[sarmate]

Comment montrer que :

On peut toujours voir comme image de toutes les fractions rationnelles sur K à une indéterminée en remplaçant l'indéterminée par les éléments de A et de B.

On voit alors que c comme si on regardait l'image par les fractions rationnelles sur K(A) à une indéterminée et que l'on remplace ensuite l'indéterminée par les éléments de B.

[yos]

On peut faire ce que dit Sarmate, mais vues les définitions dont tu disposes il faut raisonner plus simplement :
et (clair), donc .
A présent, on évite l'inclusion inverse de la façon suivante :
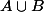
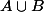
est le plus petit sous-corps de E contenant et K, or est un sous-corps de E contenant et K, donc au vu de l'inclusion précédente, on a l'égalité .

[quinto]

Il me semble que tout c'est beaucoup de bruit pour rien.
On peut clairement créer 1+i avec i et R.
Réciproquement, étant donné 1+i et R, on crée i en remarquant que i=1+i-1

Et c'est fini ...

[yos]

Je suis d'accord quinto mais la question initiale demande de prouver que
R(i)=C. Aussi évident que ça paraisse, il faut bien un argument.

[quinto]

Je suis d'accord quinto mais la question initiale demande de prouver que
R(i)=C. Aussi évident que ça paraisse, il faut bien un argument.

Mais c'est la définition de C ...

[yos]

Mais c'est la définition de C ...

C=R(i)??
Si tu me dis C=R² ou C=R[X]/(X²+1) ou encore , je veux bien, mais il faut bien aller chercher le "i" quelquepart. Une fois qu'on l'a fait, il se pose la question : quel est le plus petit sous-corps de C contenant R et i? J'ai pas dit que c'est une question compliquée, mais c'est une vraie question.

[quinto]

C=R(i)??
Si tu me dis C=R² ou C=R[X]/(X²+1) ou encore , je veux bien, mais il faut bien aller chercher le "i" quelquepart. Une fois qu'on l'a fait, il se pose la question : quel est le plus petit sous-corps de C contenant R et i? J'ai pas dit que c'est une question compliquée, mais c'est une vraie question.

Non ce n'est pas une vraie question, c'est bel et bien la définition.
Ce que l'on appelle i c'est en fait X dans R[X]/(x^2+1) et R est la classe des polynômes constants dans ce même anneau.

On ne peut pas vraiment partir de rien pour créer i. Il faut nécessairement une définition et quelque soit celle que tu te donnes, tu vois que R(i) vaut C par définition de R(i).
a+

[yos]

Ce que l'on appelle i c'est en fait X dans R[X]/(x^2+1)

Non, i est (par définition) l'image de X par la surjection canonique . C'est ça l'invention de i.

On ne peut pas vraiment partir de rien pour créer i.

Là je suis bien d'accord.

Il faut nécessairement une définition et quelque soit celle que tu te donnes, tu vois que R(i) vaut C par définition de R(i).
a+

R(i) est par définition le plus petit sous-corps de C contenant R et i (c'est la définition donnée par l'auteur de l'exercice) et rien de plus. Si tu veux plus, il faut le prouver.

[quinto]

Non, i est (par définition) l'image de X par la surjection canonique . C'est ça l'invention de i.

C'est ce que je viens de dire

Je suis d'accord avec toi, mais pour parler de R(i), il faut déjà avoir créé i, non ?

Enfin, peu importe on tourne en rond pour rien

a+

[yos]

pour parler de R(i), il faut déjà avoir créé i, non ?

Oui, c'est ce que je dis depuis le début : on construit C à partir de R. Dans C, on a un élément noté i et un corps isomorphe à R qu'on note encore R. On peut alors parler de R(i) comme sous-corps de C. Le fait que c'est égal à C est presque immédiat mais je dis que c'est pas exactement la définition de Barbu 23: voir le message 3.
Pour toi la notation R(i) désigne , ce que je comprends bien, mais ici ce n'est pas le point de vue adopté je crois.

Enfin, peu importe on tourne en rond pour rien

Je le reconnais.

[namfoodle sheppen]

j'ai juste un problème; si le corps K compris entre R et C (différent de R) est non commutatif, on ne peux pas utiliser les dimensions de R-ev pour démontrer que K=C. Alors la propriété reste-t-elle vrai si K est non commutatif ?

[Imod]

Comment un corps non commutatif pourrait être contenu dans un corps commutatif ?

Imod

[yos]

Ca reste vrai : un corps gauche est encore un ev sur son centre. Regarde les quaternions par exemple.

[yos]

Comment un corps non commutatif pourrait être contenu dans un corps commutatif ?

Imod

En plus!!!!

[barbu23]

Bonjour:
j'ai encore une question à vous poser:
Pourquoi si est algébrique alors est le polynome minimal de sur .
Comment on détermine généralement le polynome minimal d'un élément algébrique et merçi infiniment !!

[kazeriahm]

bah le polynome minimal de i ne peut etre de degré un sur R, on le cherche donc de degré 2 et unitaire...

X^2+1 convient donc c'est lui (si j'ai bien compris les notions dont on parle)

[barbu23]

Resalut:
Si on prend une classe de polynomes : .
Laquelle de ces deux assertions suivantes est correcte :
1)
2)
et merçi infiniment !!