Intégrales multiples
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 16:52
par Sylar » 26 Juin 2007, 16:52
Bonjour,j'ai un peu de mal avec les intégrales multiples d'ou la difficulté que j'ai a calculer:
int[delta]x.y.dx.dy ou :
delta={(x,y) tel que: y>=0 et (x+y)^2=<2.x/3 }
Merci....
-
sarmate
- Membre Naturel
- Messages: 84
- Enregistré le: 20 Juin 2007, 12:07
-
 par sarmate » 26 Juin 2007, 17:23
par sarmate » 26 Juin 2007, 17:23
J'ai pas trop réfléchi, mais n'a-t-on pas que :

={(x,y), 0=<y=<

; 0=<x=<2/3} ?
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 17:46
par Sylar » 26 Juin 2007, 17:46
Je vois pas comment t'obtiens ca ..... :hum:
-
sarmate
- Membre Naturel
- Messages: 84
- Enregistré le: 20 Juin 2007, 12:07
-
 par sarmate » 26 Juin 2007, 17:50
par sarmate » 26 Juin 2007, 17:50
De l'inégalité (x+y)^2=<2.x/3 tu trouves que x est positif.
Tu prends la racine carrée et tu isoles y pour obtenir :
0=<y=<

Et le membre de droite pour être positif doit vérifier 0=<x=<2/3
Ensuite est-ce que ces conditions définissent delta... ? je n'ai pas vérifié...
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 17:54
par Sylar » 26 Juin 2007, 17:54
oK MERCI BEAUCOUP ;j'ai une question pour le calcul de l'intégrale comment savoir si on intègre par rapport a x ou a y en premier....
-
sarmate
- Membre Naturel
- Messages: 84
- Enregistré le: 20 Juin 2007, 12:07
-
 par sarmate » 26 Juin 2007, 18:00
par sarmate » 26 Juin 2007, 18:00
De rien... je ne suis pas sûr que cela soit correct...
Si le delta que je t'ai donné est correct (???) tu intègres ydy entre 0 et

ce qui te donne une expression en x. Ensuite tu intègres ce résultat.
Tout cela sous réserve...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 26 Juin 2007, 18:02
par Pythales » 26 Juin 2007, 18:02
^2=\frac{2x}{3})
donne
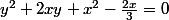
soit
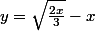
(car
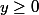
) , et

est positif entre

et
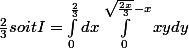
-
sarmate
- Membre Naturel
- Messages: 84
- Enregistré le: 20 Juin 2007, 12:07
-
 par sarmate » 26 Juin 2007, 18:07
par sarmate » 26 Juin 2007, 18:07
Pythales a écrit:^2=\frac{2x}{3})
donne
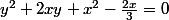
soit
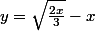
(car
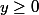
) , et

est positif entre

et
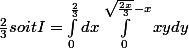
C'est en gros ce à quoi j'avais pensé, sauf que je pense que c plus rapide de prendre directement la racine carrée dans ]
^2=\frac{2x}{3})
pour obtenir y en fonction de x.
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 18:14
par Sylar » 26 Juin 2007, 18:14
Ok merci ,le reste n'est que du calcul.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 26 Juin 2007, 18:18
par kazeriahm » 26 Juin 2007, 18:18
oui enfin sylar à l'oral sur un exo de ce type tu devras savoir justifier (théorème de fubini), c'est bon?
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 18:20
par Sylar » 26 Juin 2007, 18:20
Euh pour justifier quoi ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 26 Juin 2007, 18:23
par kazeriahm » 26 Juin 2007, 18:23
pour justifier que tu intègres comme tu veux (d'avord en y puis en x)
à la base rien ne te permet de faire ca...
ici c'est facile f(x,y)=g(x)*h(y)=x*y, les variables sont "séparables", la fonction est continue et le domaine est borné donc ca se passe sans trop de soucis mais bon il faut quand meme savoir ce qu'on fait...
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 18:37
par Sylar » 26 Juin 2007, 18:37
Y a une histoire d'intégrabilité avec le théorème de Fubini....
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 26 Juin 2007, 18:54
par kazeriahm » 26 Juin 2007, 18:54
effectivement mais c'est le genre de théorème a connaitre parce qu'à l'oral, si tu tombes sur un exo du genre, étant donné que c'est calculatoire l'examinateur t'attendra sur les justifications
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 26 Juin 2007, 18:57
par Sylar » 26 Juin 2007, 18:57
Ah d'accord merci ;en fait j'aime pas trop ce théorème car les hypothèses a vérifier sont nombreuses....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
