Connexité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
july3_76
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juin 2007, 10:00
-
par july3_76 » 23 Juin 2007, 18:45
On suppose p>1. Soit c appartenant au point intérieur de I. Soient a,b appartenant a I tels que a
1)Montrer que sur tt chemin gamma reliant A à B, il existe au moins un antécédant c.
2)En déduire que c possède une infinité d'antécédants.
oui f est continue...
Je ne vois pas du tout comment résoudre cet exercice, pouvez vous m'aider?
Merci d'avance.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 23 Juin 2007, 19:15
namfoodle sheppen a écrit:f est continue ?
Sans aucun doute.
Déjà il semble que f va d'un ouvert connexe de
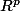
dans I (qui est un intervalle de R).
C'est amusant de faire lles hypothèses à partir des questions.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
par aviateurpilot » 23 Juin 2007, 19:51
a) soit
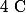
un ensemble de point formant un chemin connexe de A à B.
)
est connexe, donc
est un intervalle.
on plus
)
donc
=c)
.
b) puisqu'il y a une unfinité de chemin
_{i\in \mathbb{N}})
entre A et B
avec
\in \mathbb{N}^2;\ C_i\cap C_j=\{A,B\})
donc il y a une unfinité de solutions de
=c,\ \forall b>c>a)
-
july3_76
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juin 2007, 10:00
-
par july3_76 » 23 Juin 2007, 21:25
merci beaucoup!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
