Q(n)>q(n+1)
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 06 Juin 2007, 16:31
par aviateurpilot » 06 Juin 2007, 16:31
salut,
=E\(\frac{n}{E(\sqrt{n})}\))
soit
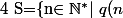>q(n+1)\})
soit
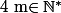
1) calculer
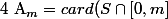)
2) s'il est possible que
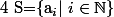
, calculer
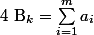
:++:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 09 Juin 2007, 16:19
par aviateurpilot » 09 Juin 2007, 16:19
personne :doh:
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 09 Juin 2007, 17:17
par alben » 09 Juin 2007, 17:17
C'est peut-être un peu trop simple. B3=26
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 09 Juin 2007, 17:23
par aviateurpilot » 09 Juin 2007, 17:23
alben a écrit:C'est peut-être un peu trop simple. B3=26
oui, c'est tres facile,
tu as raison B3=26 :++:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2007, 17:34
par aviateurpilot » 16 Juin 2007, 17:34
plus de 4 jours :doh: sans solution
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Juin 2007, 17:36
par fahr451 » 16 Juin 2007, 17:36
aviateur j 'ai proposé juste pour toi une suite sur petit jeu
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2007, 17:37
par aviateurpilot » 16 Juin 2007, 17:37
fahr451 a écrit:aviateur j 'ai proposé juste pour toi une suite sur petit jeu
je vais voir :id:
merci
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 18 Juin 2007, 13:44
par Sylar » 18 Juin 2007, 13:44
Trop dur tes sujets,désespérant a moins que je sois trop nul;pourtant je suis en mp......... :cry: :cry:
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 19 Juin 2007, 08:53
par bruce.ml » 19 Juin 2007, 08:53
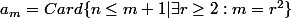
Je ne trouve pas de formulation beaucoup plus simple ...
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 23 Juin 2007, 20:09
par aviateurpilot » 23 Juin 2007, 20:09
aviateurpilot a écrit:salut,
=E\(\frac{n}{E(\sqrt{n})}\))
soit
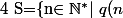>q(n+1)\})
soit
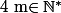
1) calculer
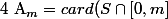)
2) s'il est possible que
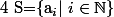
, calculer
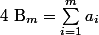
:++:
voila ma solution
\in N^*\times N;\ n=m^2+k)
avec
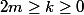
si
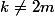
=E\(\frac{m^2+k}{m}\)=m+E(\frac{k}{m}))
=E\(\frac{m^2+k+1}{m}\)=m+E(\frac{k+1}{m})\ge q(n))
si
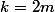
=E\(\frac{m^2+2m}{m}\)=m+2)
=E\(\frac{m^2+2m+1}{m+1}\)=m+11\}})
1)
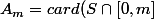=card\{h^2-1|\ h>1;\ h^2\le m+1\})
d'ou
-2})
2)
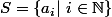
avec
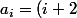^2-1)
calculer
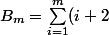^2-1=-m+\bigsum_{i=3}^{m+2}i^2=...)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité