Ker et image d'une application lineaire

[peli_123]

salut
j'ai un exo corrige provenant d'un livre mais je ne parviens pas a comprendre une etape de la resolution d'un systeme d'equation.
Dans le cadre des applications lineaires cet exercice, nous permet de trouver le ker.J'ai compris que le ker de f(x,y,z) est l'ensemble des x,y,z tel que f(x,y,z)=0
(en gros f:(x,y,z)->0)






j'ai un probleme a ce passage


comment fait on pour passer de

a


edit:emission avant le terme du sujet :we:

[peli_123]

pour mon estime personnelle tu as vu ca du premier coup?

[peli_123]

ok merci pour ta reponse

[flight]

salut

on a le systeme x+y+z= 0 (1)
3x+2y-z=0 (2)

soit 3x+3y+3z=0 (x3)
3x+2y-z = 0
soit en faisant (1) - (2) il vient y= 4z
et de (1) il decoule que x= 3z on exprime les inconnues principales en fonction des inconnues secondaires.

soit kerf={(x,y,z) appart à R^3/ (3z,4z,z )}
soit kerf=vect{(3,4,1)} et kerf est une direction vectorielle

[flight]

erreur ici:

soit kerf={(x,y,z) appart à R^3/ (3z,4z,z )}
soit kerf=vect{(3,4,1)} et kerf est une direction vectorielle

lire

soit kerf={(x,y,z) appart à R^3/ (3z,-4z,z )}
soit kerf=vect{(3,-4,1)} et kerf est une direction vectorielle

[peli_123]

quel est le ker de cette application

moi je trouve
mais en verifiant ce n'est valable que pour la premiere
equation
j'ai retranche 3 la l1 de l2
j'ai isole z par rapport a y z=7/2 *y
enfin j'ai utilise la relation z=7/2 *y dans la premiere equation
ou ai je fais l'erreur?

[sarmate]

quel est le ker de cette application

moi je trouve
mais en verifiant ce n'est valable que pour la premiere
equation
j'ai retranche 3 la l1 de l2
j'ai isole z par rapport a y z=7/2 *y
enfin j'ai utilise la relation z=7/2 *y dans la premiere equation
ou ai je fais l'erreur?

Bonjour.

Tout d'abord, le noyau d'une application linéaire est un sev de l'espace de départ, donc ici de .
Pour le trouver tu résouds le système comme tu as fait, mais il y a une erreur de calcul :

On a en fait

[peli_123]

merci de ton aide sarmate

je retranche 3 fois la ligne 1 de la ligne 2

j'isole z

je remplace z dans la premiere equation

je trouve ca

[sarmate]

lorsque tu retranches 3 fois la ligne 1 à la ligne 2 il me semble que cela donne :

7y+5z=0 et donc que

Si tu ajoutes ensuite 2 fois la ligne 1 à la ligne 2, tu obtiens :

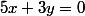
d'où

Ainsi on voit que la solution du système dépend du paramètre y (donc le noyau est de dimension 1), on remplace ensuite y par la valeur de notre choix (sauf 0) pour obtenir une base du noyau. On peut choisir y=5, ce qui donne les coordonnées que je t'ai écrites plus haut.

Ou encore tu peux écrire que les élèments du noyau sont de la forme :



Tu peux alors vérifier que de tels vecteurs vérifient bien les équations définissant le noyau.

Je peux te conseiller également, pour que tu puisses gagner du temps, d'utiliser le logiciel Maxima (qui est gratuit car sous licence GNU/GPL), tu le trouveras à l'adresse suivante :

http://sourceforge.net/project/showfiles.php?group_id=4933&package_id=4960&release_id=505664

L'utilisation en est très intuitive, et en ce qui concerne ton système il faut taper :

linsolve([x+2*y-z=0, 3*x-y+2*z=0], [x,y,z]);