salut
voici un exo dont j'ai une solution mais je crois qu'on peut faire mieux
E est un evn complet et A un ouvert borné non vide de E tel que pour tout (x,y) dans A^2, il existe une boule B contenue dans A et contenant (x,y).
Montrer que A est une boule ouverte.
Si quelqu'un a une solution...
Evn
3 messages
- Page 1 sur 1
D'abord je pense que c'est plutôt 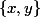 qui est dans B non ?
qui est dans B non ?
Sinon, voici ma méthode. On essaye d'abord de déterminer cette boule et on le montre par double inclusion. On commence par remarquer que A est borné donc on peut définir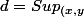\in A^2}d(x,y)) . De même, on peut définir des suites
. De même, on peut définir des suites ) et
et ) telles que
telles que ) tende vers d.
tende vers d.
On pose alors le milieu de
le milieu de  . Toutes ces suites sont bornées, on peut extraire de sorte à ce qu'elles convergent toutes. On note x,y et O les limites. On veut alors montre que A = B(O,r).
. Toutes ces suites sont bornées, on peut extraire de sorte à ce qu'elles convergent toutes. On note x,y et O les limites. On veut alors montre que A = B(O,r).
- \subset A :) il suffit de remarquer que par hypothèses,
il suffit de remarquer que par hypothèses,  \subset A) où
où 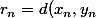) .
.
-:) soit Z un point tel que d(Z,O) > r, on peut constuire des points
soit Z un point tel que d(Z,O) > r, on peut constuire des points  sur la droite (OZ) tels que
sur la droite (OZ) tels que
 > r) ce qui est absurde.
ce qui est absurde.
Sinon, voici ma méthode. On essaye d'abord de déterminer cette boule et on le montre par double inclusion. On commence par remarquer que A est borné donc on peut définir
On pose alors
-
-
bon c'est ce que j'ai fait modulo les différences de raisonnement (par exemple au lieu de considèrer tes suites (xn) et (yn) du début j'avais pris (an) tq B(a_n,R-1/n) contenu dans A avec R le sup des rayons tel qu'il existe une boule de ce rayon contenu dans A, on montre a_n de Cauchy,....) ca revient globalement au meme.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
