Une question

par **sue** » 16 Juin 2007, 17:08

Bonjour,

j'ai une question mais je ne sais pas vraiment à quoi renvie mon problème ... en fait j'ignore ce comment on appelle cette 'opération' en français .

par ex quand on fait le passage :

ça me bloque , je ne trouve pas le mot , j'espère que vous avez compris de quoi je parle .

bref ma question est la suivante : y-a-t-il une méthode générale pour réaliser cet 'opération' ? parce que ce n'est pas toujours évident .

merci

par **yos** » 16 Juin 2007, 17:30

1. Décomposition en éléments simples.
2. Oui, méthodes il y a.

par **fahr451** » 16 Juin 2007, 17:34

notez le S

yos a plus d 'un tour dans son sac

par **sue** » 16 Juin 2007, 17:45

merci pour le terme .

ça m'interesse de savoir une , la plus simple et efficace .

merci

par **yos** » 16 Juin 2007, 18:11

sue a écrit: la plus simple et efficace .

et qui fait le café aussi?

Non mais c'est pas évident, regarde un bouquin parce que avant d'avoir une méthode, il faut connaître le résultat théorique qui te dit la forme générale de la DES. Et là c'est variable selon que le corps de base est R ou C. De plus l'énoncé est un peu lourd si le dénominateur de ta fraction possède des racines multiples.
Pour faire simple, imaginons un quotient de deux polynômes

où Q(x) n'a que des racines simples dans C.
1) on divise P(x) par Q(x) :
P(x)=Q(x)A(x)+R(x) avec degR(x)<degQ(x).
On est ainsi ramené à

, bref au cas de figure où le degré du numérateur est plus petit que celui du dénominateur.

2) On sait que

où les

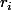
sont les n racines distinctes de Q(x).
Reste à trouver les réels

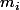
. Pour ça tu multiplies les deux membres par

et après simplification à droite tu remplace x par

.

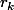
par **fahr451** » 16 Juin 2007, 18:14

je m y colle

la fraction est

P/Q Pet Q deux polynômes sans racine commune
les racines de Q sont appelés les pôles

la multiplicité d'un pôle a est celle de a comme racine de Q

on a
dans C Q se factorise complètement
P/Q = somme d éléments simples

éléments simples =

* partie entière = polynôme = quotient de P par Q

*constante / (x-a)^k avec a pôle d e multiplicité n et
k entier 1=< k =
technique quand les pôles sont simples
on écrit A PRIORI la décomposition avec des coeffs inconnus

on veut le terme en c/(x-a)

on multiplie par (x-a)

on simplifie par (x-a) dans Q

on évalue en a
on obtient c directement

quand les pôles sont multiples (de multiplicité importante)

la division suivant le s puissances croissantes est utile

sinon on peut aussi évaluer en qq points et résoudre un système

par **fahr451** » 16 Juin 2007, 18:15

mince grillé

mais j'ai évoqué la division suivant les puissances croissantes

par **sue** » 16 Juin 2007, 20:09

oui , merci à vous , en même temps j'ai regardé une vidéo sur la DES et celà me confirme bcp de choses .
je comprends maintenant la méthode au cas des pôles simples sinon au cas d'une multiplicité importante , je vais regarder encore d'autres liens et je vous tiens au courant au cas ou je bloque .

par **fahr451** » 16 Juin 2007, 21:46

Rain' a écrit:Et tu as déjà eu à t'en servir en réalité ?

bien sûr en réalité (pas pour acheter mon pain) à une époque où elle était monnaie courante y compris dans les dls

par **fahr451** » 17 Juin 2007, 08:45

c'est 30% des exos de prépa les exos de calcul même si aujourd 'hui
la virtuosité est bien moindre.
0n peut considérer que c'est bête et méchant (car raisonnement nul) mais savoir organiser et mener un calcul demande des qualités que certains très forts n'ont pas nécessairement , et d'ailleurs ta remarque laisse supposer que ce n'est pas forcément ce avec quoi tu es le plus à l'aise.

par **kazeriahm** » 17 Juin 2007, 11:50

on peut aussi multiplier par des monomes et regarder la limite en l'infini pour obtenir des relations entre les constantes

par **sue** » 17 Juin 2007, 23:32

merci , j'avais pas remarqué qu'il y a d'autres réponses , je vais regarder tout ça tranquillement demain matin .
mais déjà en regardant un lien sur le même sujet , il y a une chose que je ne comprend pas : ça veut dire quoi 2 polynomes premiers entre eux ?

par **fahr451** » 17 Juin 2007, 23:34

sans diviseur commun autre que les constantes

par **sue** » 17 Juin 2007, 23:37

ok , y a t il une extention du th de bezout au cas des polynomes ?

par **xunil** » 17 Juin 2007, 23:45

oui: si deux polynomes P et Q sont 1ers entre eux, alors il existe 2 polynomes U et V tq:
PU+QV=1

par **sue** » 17 Juin 2007, 23:50

oui justement , ça confirme ce que je viens de lire . merci

par **fahr451** » 17 Juin 2007, 23:54

en gros "toute" l arithmétique des entiers se généralise à celle des polynômes

par **sue** » 18 Juin 2007, 16:33

ok
sinon,

Rain' a écrit:Dans certains cas si le polynôme est une fonction paire pensez à remplacer x par -x pour obtenir des relations simples entre les coefficients cherchés, de la même manière penser à la conjugaison.

merci Rain' , j'ai essayé avec des ex en utilisant ce tu m'as cité et ça marche bien .
juste pour ce point là concernant la parité de la fraction et aussi la conjugaison , comment peut on l'exploiter ? peux tu me donner un ex stp ?

merci

par **sue** » 18 Juin 2007, 16:55

d'accord , je vois mieux là .

et pour la conjugaison ?

par **sue** » 18 Juin 2007, 16:56

OK , ça marche . merci

Une question

une question

Qui est en ligne